构造
构造题是一种形式灵活多样的题型。正是因为这个特点,使得构造题没有一种通用的方法。
P3599 Koishi Loves Construction
题目描述
Koishi 决定走出幻想乡成为数学大师!
Flandre 听说她数学学的很好,就给 Koishi 出了这样一道构造题:
Task1:试判断能否构造并构造一个长度为 n 的 1…n 的排列,满足其 n 个前缀和在模 n 的意义下互不相同。
Task2:试判断能否构造并构造一个长度为 n 的 1…n 的排列,满足其 n 个前缀积在模 n 的意义下互不相同。
按照套路,Koishi 假装自己根本不会捉,就来找你帮忙辣。
输入格式
第一行两个整数 X 和 T,分别表示 Task 类型和测试点内的数据组数。
接下来 T 行,每行一个整数表示每组数据中的 n。
输出格式
为了方便 SPJ 的编写,您需要遵从以下格式输出。
对于每组数据仅包含一行输出:
- 如果您认为当前数据不存在符合题意的构造,只需输出一个整数 0。
- 如果您认为当前数据存在符合题意的构造却不会构造,只需输出一个整数 1。
- 如果您认为当前数据存在符合题意的构造并成功构造,则需要先输出一个整数 2,再输出 n 个整数表示构造的方案。
每两个整数之间需要有空格作为分隔符。
样例 #1
样例输入 #1
1 | 1 1 |
样例输出 #1
1 | 2 8 7 6 5 4 3 2 1 |
样例 #2
样例输入 #2
1 | 2 1 |
样例输出 #2
1 | 2 1 2 3 5 10 6 7 4 9 8 11 |
提示
对于每组数据:
- 如果您对于构造的存在性判断正确,您将会得到 30% 的分数,若您的构造符合题意或者确实不存在符合题意的构造,您将会得到剩余的 70% 的分数。
- 如果您对于构造的存在性判断不正确,您将不会得到任何分数。
对于每组测试点,您的得分将是本组数据点中得分的最小值。
测试点类型 1:10 分,满足 X = 1,1 ≤ n ≤ 10。
测试点类型 2:40 分,满足 X = 1,1 ≤ n ≤ 105。
测试点类型 3:10 分,满足 X = 2,1 ≤ n ≤ 10。
测试点类型 4:40 分,满足 X = 2,1 ≤ n ≤ 105。
对于所有测试点,满足 1 ≤ T ≤ 10。
解题思路
解答代码
P5441 【XR-2】伤痕
题目背景
长日尽处,我来到你的面前,你将看见我的伤痕,你会知晓我曾受伤,也曾痊愈。——泰戈尔《深爱你这城》
题目描述
X 国经历了一场前所未有的大地震,人们伤痕累累,整个国家破碎不堪。
为了帮助人们痊愈,也为了让 X 国能够生存下去,X 国国王决定重建 X 国。
国王决定先建造 n 座城市,由于国王喜欢奇数,所以 n 为奇数。
城市建造完后,需要给每两座城市之间都修建一条道路,即一共需要修建 $\frac{n(n-1)}{2}$ 条道路。
不过,修建双向道路的成本太高了,建造完 n 座城市后剩下的经费最多只够修建 n 条双向道路,而其余的道路只能修建成单向的。好在方向并不会影响修建单向道路所需的费用,因此所有单向道路的方向可以任意决定。
另外,等到重建完成后,国王决定将 4 座城市钦定为 X 国的核心城市。为促进 X 国的发展,这 4 座核心城市中的任意两座城市,必须能够在不经过非核心城市的情况下相互到达。
国王希望,你能够给他一种道路修建方案,使重建完成后选择 4 座核心城市的方案数最大化。
输入格式
一行一个正整数 n(1 ≤ n ≤ 99),保证 n 为奇数,表示有 n 座城市。
输出格式
第一行包含一个整数,表示最大的选择 4 座核心城市的方案数。
接下来的 n 行每行 n 个正整数描述一个邻接矩阵,表示你的道路修建方案。
具体来说,第 i 行的第 j 个数为 1 表示第 i 座城市可以通过一条道路到达第 j 座城市,为 0 表示第 i 座城市无法通过一条道路到达第 j 座城市。我们分为 3 种情况详细说明:
- i, j 之前的道路为一条 i 到 j 的单向道路,则邻接矩阵的第 i 行第 j 个数为 1,第 j 行第 i 个数为 0。
- i, j 之间的道路为一条双向道路,则邻接矩阵的第 i 行第 j 个数和第 j 行第 i 个数均为 1,你需要保证最多修建 n 条双向道路。
- i = j,则第 i 行第 j 个数(第 j 行第 i 个数)为 0。
样例 #1
样例输入 #1
1 | 3 |
样例输出 #1
1 | 0 |
样例 #2
样例输入 #2
1 | 5 |
样例输出 #2
1 | 5 |
提示
【样例 1 说明】
由于一共只有 3 个点,所以选择 4 座核心城市的方案数一定为 0,那么只需要保证修建方案满足条件即可。
【样例 2 说明】
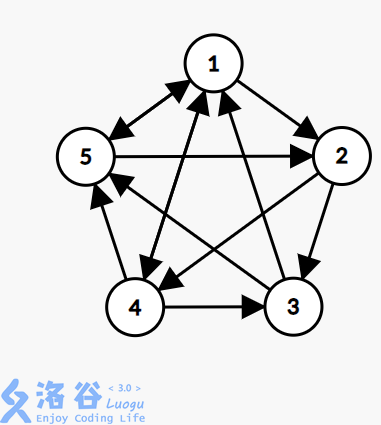
显然,在 5 个点中任意选 4 个点,都满足核心城市的条件,因此方案数最大为 5。
【数据规模与约定】
本题一共有 50 个测试点,每个测试点 2 分。对于第 i 个测试点,n = 2i − 1。
对于每个测试点,有五种可能的结果:
- 输出格式错误,包括:没有输出最大方案数、没有输出邻接矩阵、输出了多余的信息等。你将无法得到该测试点的任何分数,同时我们无法确定 Special Judge 的返回结果。
- 没有正确计算最大方案数,即使构造的道路修建方案是正确的。你将得到该测试点 0% 的分数(即 0 分),Special Judge 将会返回 WA 的结果,同时输出 “The answer is wrong.”
- 正确计算了最大方案数,但是构造的道路修建方案不满足条件,包括:邻接矩阵中有不为 0 或 1 的数、有自环、有两座城市中没有道路、有多于 n 条双向道路等。你将得到该测试点 50% 的分数(即 1 分),Special Judge 将会返回 WA 的结果,同时输出 “The answer is correct, but your plan breaks the rules.”
- 正确计算了最大方案数,构造的道路修建方案满足条件但没有将选择 4 座核心城市的方案数最大化。你将得到该测试点 50% 的分数(即 1 分),Special Judge 将会返回 WA 的结果,同时输出 “The answer is correct, but your plan is wrong.”
- 正确计算了最大方案数,同时正确构造了道路修建方案。你将得到该测试点 100% 的分数(即 2 分),Special Judge 将会返回 AC 的结果,同时输出 “The answer is correct.”
解题思路
解答代码
P5595 【XR-4】歌唱比赛
题目背景
赛时提醒:本题不提供任何关于样例 4 以及无解的解释。
赛时提醒:本题不提供任何关于输出格式以及 Special Judge 的解释。
赛时提醒:抱歉,本题的 Special Judge 不忽略行末空格,请保证两行中没有多余字符。
赛时提醒:非常抱歉,本题输入数据是 Windows 格式,而非 Linux
格式,所以在末尾的 \n 之前有一个多余的 \r
字符。请使用 scanf 或 cin 读入数据,而非
getline,因为后者会多读入一个
\r。
题目描述
小 X 参加了一场歌唱比赛。
经过一路鏖战,小 X 终于挺进了决赛,他的对手是小 Y。
这场歌唱比赛的冠军是由点赞数决定的,谁的点赞数高,谁就能夺冠。
小 X 和小 Y 依次演唱完自己的最后一首歌曲后,他们最终的点赞数确定了下来。
揭晓冠军的时刻终于到来了,主持人为了增加悬念,决定从小 X 与小 Y 的点赞数的最后一位开始,依次比较。
比如,小 X 的点赞数是 37,小 Y
的点赞数是 28。首先比较最后一位,小 X
是 7,小 Y 是 8,此时小 Y 暂时领先。再加上前一位,小 X 是
37,小 Y 是 28,此时小 X 暂时领先。比较结束,如果我们用
X 代表小 X 暂时领先,Y 代表小 Y
暂时领先,那么可以写下一个字符串 XY。
再比如,小 X 的点赞数是 137,小 Y
的点赞数是 47。如果我们再用
Z 表示小 X 与小 Y 的点赞数暂时一样,那么写下的字符串应该为
XYZ。
你作为一个精通 OI 的神仙,自然知道这种比较方式是非常不科学的,这样只是在无端拖延时间罢了,但是你却对最后写下的这个字符串很感兴趣。
现在,你得到了这个最后写下的字符串,你需要构造出一种可能的小 X 与小 Y 的点赞数。
当然,有可能不存在任何一种情况的点赞数满足这个字符串,那么你只需要输出
-1 即可。
为了方便你输出,请用前导零来补足位数。
输入格式
一行一个字符串 s,表示最后写下的字符串。
输出格式
如果有解:
- 第一行一个整数,表示小 X 的点赞数。
- 第二行一个整数,表示小 Y 的点赞数。
如果无解:
- 一行一个整数
-1。
样例 #1
样例输入 #1
1 | XY |
样例输出 #1
1 | 37 |
样例 #2
样例输入 #2
1 | XYZ |
样例输出 #2
1 | 137 |
样例 #3
样例输入 #3
1 | ZZZZZZ |
样例输出 #3
1 | 000000 |
样例 #4
样例输入 #4
1 | XYZXYZ |
样例输出 #4
1 | -1 |
提示
本题采用捆绑测试。
- Subtask 1(11 points):len(s) = 1。
- Subtask 2(42 points):si ∈ {
X,Y}。 - Subtask 3(21 points):数据保证有解。
- Subtask 4(26 points):无特殊限制。
对于 100% 的数据,si ∈ {X, Y, Z},1 ≤ len(s) ≤ 106。