『论文笔记』Feature Stylization and Domain-aware Contrastive Loss for Domain Generalization

Information

Title: Feature Stylization and Domain-aware Contrastive Loss for Domain Generalization
Author: Seogkyu Jeon 等
Institution: Department of Computer Science Yonsei University, South Korea(韩国延世大学计算机科学系)
Year: 2021
Journal: ACMMM 2021 Oral
Source: Github, Arxiv
Cite: Jeon, Seogkyu, et al. “Feature stylization and domain-aware contrastive learning for domain generalization.” Proceedings of the 29th ACM International Conference on Multimedia. 2021.
Idea: 提出了一种特征风格化模块(拓展风格)和域感知对比损失函数，用于域泛化任务

@inproceedings{jeon2021stylizationDG,
  title={Feature Stylization and Domain-aware Contrastive Learning for Domain Generalization},
  author={Seogkyu Jeon and Kibeom Hong and Pilhyeon Lee and Jewook Lee and Hyeran Byun},
  booktitle={The 29th ACM International Conference on Multimedia},
  year={2021},
}

Introduction

一些关键点：

域泛化性与训练用的域数量成正比：有些使用生成式的方法来生成新域用于训练，但
1. 基于 GAN 的方法随着域数量增加难以优化
2. 基于 AdaIN 的方法无法保留图像语义信息，因为 IN 会消除类判别信息
该文章的贡献
1. 提出了一种域泛化框架：使用特征风格化模块生成利用不同域风格
2. 提出一种域感知对比损失，通过对比域标签和类标签增强域不变性
3. 实验表明效果很好~

Method

首先是分类的交叉熵损失（K 是源域数量）： $$ \mathcal{L}_{ce} = - \frac{1}{K}\sum_{i=1}^{K} \frac{1}{n_i} \sum_{j=1}^{n_i}y^i_j\log(p(\Phi(x^i_j))), $$ 总的思路其实也很简单，生成更多不同域的样本。作者的做法是利用统计特征来生成新的增强域，并保证生成的特征保持原始语义。借助模型特征分解，将结构特征与纹理特征分为高频和低频分量，特征分解： $$ \begin{aligned} z^L_{l} &= \text{UP}(\text{AvgPool}(z_{l})), \\ z^H_{l} &= z_{l} - z^L_{l}, \end{aligned} $$ AvgPool 是大小为 2 的空间平均池化操作，UP 是最邻近上采样。接下来通过统计数据进行风格化，先求均值方差： $$ \begin{aligned} \mu^{L}_{l} &= \frac{1}{BH_{l}W_{l}}\sum_{m=1}^{BH_{l}W_{l}} flat(z^L_{m,l}),\\ (\sigma^L_{l})^2 &= \frac{1}{BH_{l}W_{l}}\sum_{m=1}^{BH_{l}W_{l}} (flat(z^L_{m,l}) - \mu^L_{l})^2, \end{aligned} $$ 其中 flat(⋅) : ℝ^{B × C_l × H_l × W_l} → ℝ^{BH_lW_l × C_l} 是展开操作，μ_l^L, σ_l^L ∈ ℝ^C_l 表示特征风格的均值和方差。这些数据与域特征高度相关，接下来再计算统计量的均值和方差 $$ \begin{split} \hat{\mu}^L_{l} &= \frac{1}{C_{l}}\sum_{c=1}^{C_{l}} \mu_{c,l}^L,\;\;\;\; (\hat{\sigma}^L_{c,l})^2 = \frac{1}{C_{l}}\sum_{c=1}^{C_{l}} (\mu_{c,l}^L - \hat{\mu}^L_{l})^2,\\ \tilde{\mu}^L_{l} &= \frac{1}{C_{l}}\sum_{c=1}^{C_{l}} \sigma_{c,l}^L,\;\;\;\; (\tilde{\sigma}^L_{c,l})^2 = \frac{1}{C_{l}}\sum_{c=1}^{C_{l}} (\sigma_{c,l}^L - \tilde{\mu}^L_{l})^2, \end{split} $$ 接下来，使用缩放参数s_μ 和 s_σ 生成新的风格向量： $$ \begin{split} \mu^{\text{new}}_l \sim \mathcal{N}(\hat{\mu}^L_{l}, s_\mu (\hat{\sigma}^L_{l})^2), \\ \sigma^{\text{new}}_l \sim \mathcal{N}(\tilde{\mu}^L_{l}, s_\sigma (\tilde{\sigma}^L_{l})^2). \end{split} $$ 再将生成的风格向量应用于源低频分量 z_l^L： $$ \bar{z}^L_l = \sigma^{\text{new}}_l \left ( \frac{z^L_l - \mu^{L}_l}{\sigma^{L}_l} \right ) + \mu^{\text{new}}_l. $$ 再重新组合低频和高频： z̄_l = z_l^H + z̄_l^L. z̄_l 同样通过网络中的其他层，并对输出进行一致性约束： $$ \mathcal{L}_{cons} = - \frac{1}{K}\sum_{i=1}^{K} \frac{1}{n_i} \sum_{j=1}^{n_i}p(\Phi(x^i_j), \tau)\log(p(\bar{\Phi}(x^i_j))), \\~0 \leq \tau \leq 1, $$ p 是 softmax 函数，Φ̄(x_jⁱ) 是网络输出。

将风格化特征作为正样本，其他样本作为负样本，对比学习的公式定义为： $$ \mathcal{L}_{sup} = - \sum_{i \in I} \frac{1}{|P(i)|} \sum_{p \in P(i)}\log~\frac{exp(f'_i \cdot f'_p / \tau)}{\sum_{a \in A(i)}exp(f'_i \cdot f'_a / \tau)}, $$ P(i) 表示正样本的索引，f^′ 表示特征提取器接 L2 正则化的输出，但直接使用效果不好，作者解释是这样会让特征空间变得具有域特异性。作者提出： $$ \mathcal{L}_{dsup} = - \sum_{i \in I} \frac{1}{|P(i)|} \sum_{p \in P(i)}\log~\frac{exp(f'_i \cdot f'_p / \tau)}{\sum_{a \in P(i) \cup D(i)}exp(f'_i \cdot f'_a / \tau)}, $$ 其中 D(i) 是与锚点相同域标签的样本。

图里面说的比较清晰，就是排除掉不同域之间负样本的互斥。

总的损失函数为 ℒ = ℒ_ce + λ_consℒ_cons + λ_dsupℒ_dsup,

Experiment

主要是多源域的实验，这里就贴个 PACS 的吧

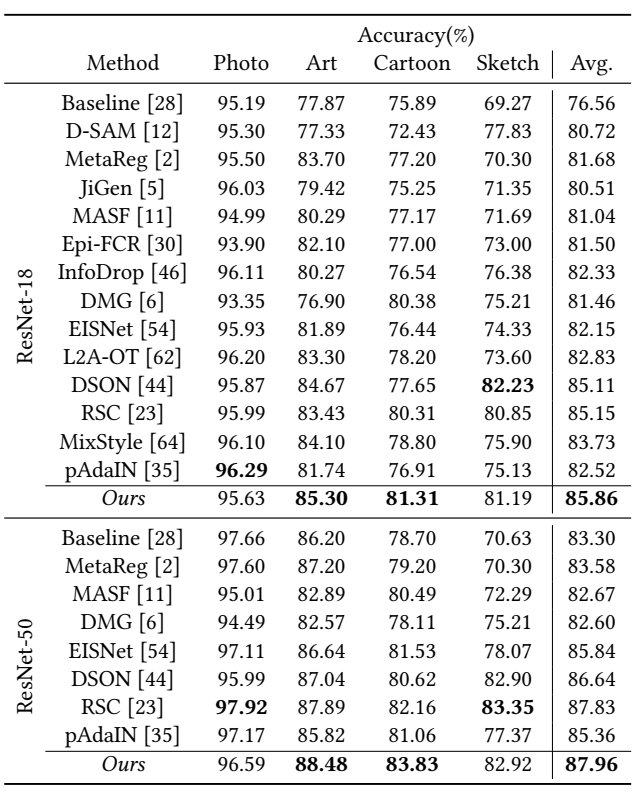
作者表示也可以用在单源域，忽略 D(i) 就行。

消融实验这里就不列了，可以去看看原文

Conclusion

利用低频特征的特征风格的统计值来控制生成风格化的样本，并提出一个域感知对比损失。

感觉解释比较主观，实验中也缺少对 motivation 的更进一步的解释和验证。

如有错漏，欢迎指正！如果对你有帮助的话，请给我点个赞吧~

欢迎前往我的博客查看更多笔记