『论文笔记』Adversarially Adaptive Normalization for Single Domain Generalization

Information

Title: Adversarially Adaptive Normalization for Single Domain Generalization
Author: Xinjie Fan, Qifei Wang, Junjie Ke, Feng Yang, Boqing Gong, Mingyuan Zhou
Institution: 谷歌
Year: 2021
Journal: CVPR
Source: open access，Arxiv
Cite: Xinjie Fan, Qifei Wang, Junjie Ke, Feng Yang, Boqing Gong, Mingyuan Zhou; Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2021, pp. 8208-8217
Idea: 针对 BN 的统计量不适合跨域任务的缺点提出自适应的正则化方法

@InProceedings{Fan_2021_CVPR,
    author    = {Fan, Xinjie and Wang, Qifei and Ke, Junjie and Yang, Feng and Gong, Boqing and Zhou, Mingyuan},
    title     = {Adversarially Adaptive Normalization for Single Domain Generalization},
    booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
    month     = {June},
    year      = {2021},
    pages     = {8208-8217}
}

Abstract

针对单源域泛化，在对抗域增强(adversarial domain augmentation, ADA)^[3] 训练中，提出了自适应标准化和缩放正则化(adaptive standardization and rescaling normalization, ASR-Norm)，通过神经网络学习标准化和缩放统计量。

Introduction

单源域泛化，就是在一个源域训练在没见过的目标域测试。

很多工作研究了对抗域增强(ADA)，即使用对抗的方法来模拟目标域以学习域不变特征来提高模型的泛化性能。该工作在 ADA 框架的基础上构建自适应归一化来提高模型的泛化性能。

提出方法的动机是在现有的单源域泛化中使用的 BN 中的指数移动平均（EMA）是在训练数据集上统计得到的，缺乏域泛化性能，目标域的统计量通常与源域不一样，所以不能很好的适用在目标域。BN-Test 提出将 BN 的指数移动平均也加上目标域，但这需要目标域数据并且训练效果也依赖于测试的 batch size。

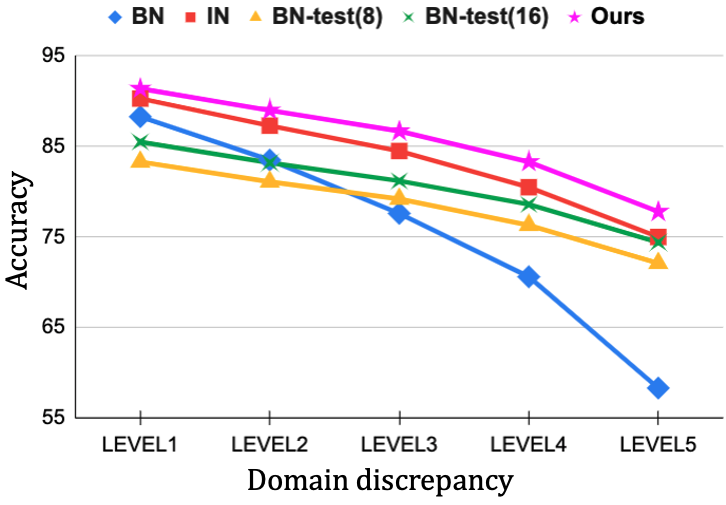
上图展示了单源域泛化上五种正则化方法在 CIFAR-10-C的对比，Level 表示原图的差异程度。这表明有必要探究对 BN 的改进。

作者提出的自适应标准化和重缩放正则化（ASR-Norm）是针对每个独立输入样本进行自适应标准化和缩放统计量的方法。该方法通过近似优化鲁棒目标对统计量进行正则化，使得统计量能自适应来自不同域的数据，从而使模型具备更好的与泛化性能。同时，该方法可以视为传统的正则化包括 BN, IN, LN, GN, SN(Switchable Normalization) 在内的通用形式。

这篇文章的主要贡献有：

提出了一种新的自适应正规化方法，弥补了 ADA 中正则化方法域泛化的缺陷，并且是目前首先提出同时学习标准化和重缩放统计量的正规化方法
效果很好

Method

框架

为了更好的提高模型的泛化性能，有论文^[1]提出了一种考虑源域 P_s 最坏情况下的鲁棒目标： ℒ_R(θ) := sup_{P : D(P, P_s) ≤ ρ}𝔼_{{X, Y} ∼ P}[l(θ; X, Y)] 其中，θ 表示模型参数， l : 𝒳 × 𝒴 → ℝ 是损失函数，D(P, Q) 表示域分布的距离度量，该目标能让模型在距离源域分布 P_s 在 ρ 距离内表现良好，但很难优化。但可以通过将其转换为带有惩罚项 η 的拉格朗日优化问题并通过最小最大化方法进行求解： ℒ_RL := sup_P{𝔼_P[l(θ; (X, Y))] − ηD(P, P_s)} 这里通过 Wasserstein 距离定义两个分布之间的距离 D ，梯度 ℒ_RL 在适当的条件下可以写为 ∇_θL_RL = 𝔼_{(X, Y) ∼ P_s}[∇_θl(θ; (X_η^*, Y))]，其中 X_η^* := argmax_{x ∈ 𝒳}{l(θ; (x, Y)) − ηc_θ((x, Y)), (X, Y))} 而 c_θ 是 𝒳 × 𝒴 空间学习到的距离度量。梯度上升被提出来寻找近似 X_aug 到 X_η^* ，它最大化预测损失 l，同时保持与原始图像 X 的紧密语义距离。然后将合成图像 X_aug 及其标签附加到训练数据集。这个阶段被称为最大化阶段，与最小化阶段交替出现，我们优化 θ 以最小化原始数据和扩充数据的预测损失。

简单来说就是用原图生成对抗样本当做一个新的“对抗域”然后丢到源域里面去一起训练

ASR-Norm

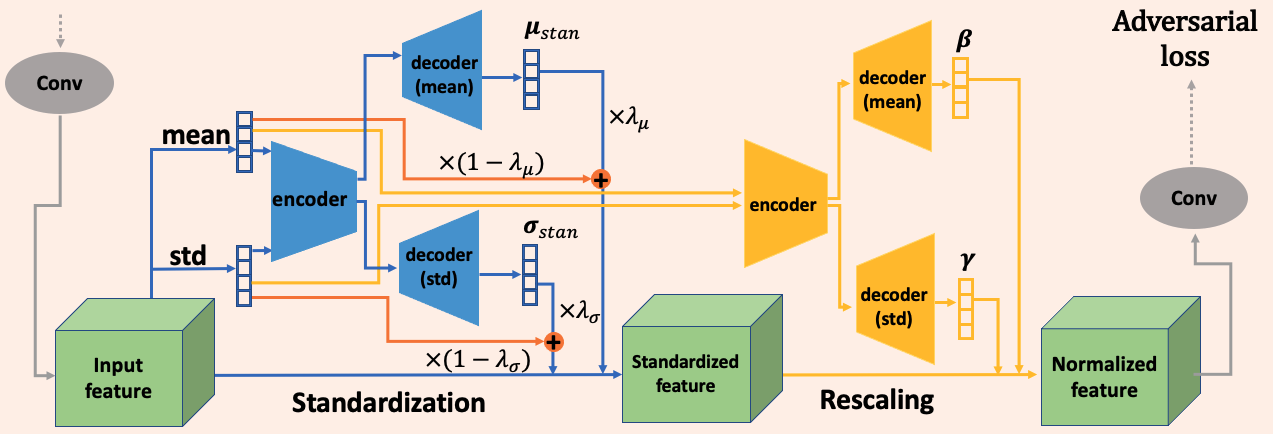
对于 Normalization，定义输入 x ∈ ℝ^{C × H × W}, 其标准化的均值和方差为 μ_stan, σ_stan ∈ ℝ^C ，进行标准化操作得到的 x_stan 使用 γ, β ∈ ℝ^C 进行缩放操作 $$ \begin{cases} x_\text{stan} = (x - \mu_\text{stan}) / (\sigma_\text{stan} + \epsilon),\\ x_\text{norm} = x_\text{stan} * \gamma + \beta. \end{cases} $$ ASR-Norm 使用自动编码器结构的神经网络，对于每个输入样本独立构建自适应的计算图，并且在标准化中引入了残差项用于稳定学习过程。

AS

AS(Adaptive Standardization) 即自适应标准化：即对于输入 x 计算： μ_stan = f(x), σ_stan = g(x) 这个可以概括大多数正则化方法，BN，GN，IN，SN 等，即 f 和 g 不同，具体是什么文章有列表说，这里就不赘述了。作者认为这些方法太严格了，限制了灵活性，所以提出用神经网络来学习 f 和 g 来获得更具有一般性的标准化方法。

首先我们需要计算 μ_stan, σ_stan，为了减少计算量，使用元素特征图逐通道的均值和标准差作为输入而不是 feature map 来学习标准化统计值。 $$ \begin{cases} \mu_c = \sum_{i=1}^H\sum_{j=1}^W x_{cij} / (H\times W),\\ \sigma_c = \sqrt{\sum_{i=1}^H\sum_{j=1}^W (x_{cij} - \mu_c)^2 / (H\times W)} \end{cases} $$ 作者使用编码器-解码器(encoder-decoder) 结构来从 μ, σ 学习 μ_stan, σ_stan，其中编码器提取通过所有通道的内部关系提取全局信息，解码器学习分解每个通道的信息，具体实现为一个简单的全连接层： $$ \begin{cases} \mu_\text{stan} = f(x) := f_\text{dec}(\text{ReLU}(f_\text{enc}(\mu))),\\ \sigma_\text{stan} = g(x) := \text{ReLU}(g_\text{dec}(\text{ReLU}(g_\text{enc}(\sigma)))) \end{cases} $$ 其中 f_⋅(), g_⋅() 表示全连接层，编码器将输入映射到隐藏空间 ℝ^C_stan 解码器将其映射回空间 ℝ^C, 且有 C_stan < C. 作者称在实践的时候发现共享 μ_stan, σ_stan 的编码器参数不影响结果还节省参数量，所以 f_enc = g_enc.

残差学习

在训练的早期阶段，标准化网络的学习阶段会出现不稳定并导致数值问题，例如 σ_stan 很小导致 x_stan 很大，作者考虑过添加带有边界约束的激活函数 sigmoid 但这会导致对 x_stan 较大的样本的性能损失，为了灵活控制，作者引入了残差项用于正规化： $$ \begin{cases} \mu_\text{stan} = \lambda_\mu f_\text{dec}(\text{ReLU}(f_\text{enc}(\mu))) + (1- \lambda_\mu) \mu,\\ \sigma_\text{stan} = \lambda_\sigma \text{ReLU}(g_\text{dec}(\text{ReLU}(g_\text{enc}(\sigma))) + (1- \lambda_\sigma) \sigma. \end{cases} $$ 其中 λ_μ, λ_σ 是可学习的参数并用 sigmoid 约束到 [0, 1] 之间，在早期阶段都初始化为一个很小的值以便在训练的前期阶段能保证网络训练的稳定性，后期会逐渐增大以学习到的统计量为主。

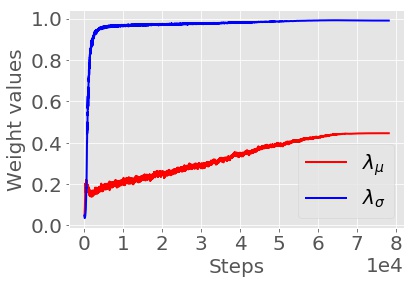
(WRN 对 CIFAR-10-C 的测试)

AS 的所有操作都是样本独立的，不同样本之间没有依赖关系，其计算图在训练和测试过程是一致的。

AR

AR(Adaptive Rescaling) 即自适应重缩放。

通常我们使用可学习参数 γ, β ∈ ℝ^C 来对标准化输出 x_stan 进行缩放操作，这对所有样本都是相同的。有论文^[2]指出具有样本依赖的重缩放参数有更好的性能。据此作者提出构建自适应重缩放网络。

类似标准化网络，重缩放参数也是来源于统计量 μ, σ: $$ \begin{cases} \beta = \psi(x) := \text{tanh}(\psi_\text{dec}(\text{ReLU}(\psi_\text{enc}(\mu)))) + \beta_\text{bias},\\ \gamma = \phi(x) := \text{sigmoid}(\phi_\text{dec}(\text{ReLU}(\phi_\text{enc}(\sigma)))) + \gamma_\text{bias}, \end{cases} $$ 其中 ϕ_enc, ϕ_dec, ψ_enc, ψ_dec 都是全连接层，同样有隐藏空间维度 C_rescale < C 和 ϕ_enc = ψ_enc，另外 γ_bias, β_bias ∈ ℝ^C 初始化为 0 和 1.

Experiment

实验设置：

数据集
- DIgits：包括 MNIST, SVHN, MNIST-M, SYN, USPS, 使用 MNIST 作为源域
- CIFAR-10-C：在 CIFAR-10 上进行训练
- PACS：两种方法：单源域或多源域（三个源域一个目标域，直接混合训练）
超参数
- C_stan, C_rescale 设置为 C/2, C/16, λ_μ, λ_σ 初始化为 sigmoid(−3).
模型：ConvNet(Digits), WRN(CIFAR-10-C), ResNet18(PACS)

作者发现直接将 pretrain 模型的 BN 替换为 ASR-Norm 效果不好，所以又用原先的思路添加了一个可学习权重： $$ \begin{cases} \beta = \psi(x) = \lambda_\beta \text{tanh}(\psi_\text{dec}(\text{ReLU}(\psi_\text{enc}(\mu)))) + \beta_\text{bias},\\ \gamma = \phi(x) = \lambda_\gamma \text{sigmoid}(\phi_\text{dec}(\text{ReLU}(\phi_\text{enc}(\sigma)))) + \gamma_\text{bias}, \end{cases} $$ λ_β, λ_γ 都初始化为 sigmoid(−5)，而 β_bias, γ_bias 是从预训练模型中复制过来的。

Other

结果复现

代码部分

作者没有给出开源代码，下面的代码是根据论文自行编写的代码

class ASRNorm(nn.Module):
    def __init__(self, num_channel, stan_sep=2, rsc_sep=16, eps=1e-5, init_beta=None, init_gamma=None):
        super(ASRNorm, self).__init__()
        self.num_channel = num_channel
        self.stan_mid_channel = self.num_channel // stan_sep
        self.rsc_mid_channel = self.num_channel // rsc_sep
        self.eps = eps

        self.relu = nn.ReLU(True)
        self.tanh = nn.Tanh()
        self.sigmoid = nn.Sigmoid()

        self.stan_encoder = nn.Linear(self.num_channel, self.stan_mid_channel)
        self.rsc_encoder = nn.Linear(self.num_channel, self.rsc_mid_channel)

        # standardization
        self.stan_mean = nn.Sequential(
            self.relu,
            nn.Linear(self.stan_mid_channel, self.num_channel) # stan_decoder
        )
        self.stan_std = nn.Sequential(
            self.relu,
            nn.Linear(self.stan_mid_channel, self.num_channel), # stan_decoder
            self.relu
        )
        # Rescaling
        self.rsc_beta = nn.Sequential(
            self.relu,
            nn.Linear(self.rsc_mid_channel, self.num_channel), # Rescaling_decoder
            self.tanh
        )
        self.rsc_gamma = nn.Sequential(
            self.relu,
            nn.Linear(self.rsc_mid_channel, self.num_channel), # Rescaling_decoder
            self.sigmoid
        )

        self.lamb_mu = Parameter(torch.empty(1))
        self.lamb_sigma = Parameter(torch.empty(1))
        self.lamb_beta = Parameter(torch.empty(1))
        self.lamb_gamma = Parameter(torch.empty(1))
        self.bias_beta = Parameter(torch.empty(self.num_channel))
        self.bias_gamma = Parameter(torch.empty(self.num_channel))

        # init lambda and bias
        with torch.no_grad():
            init.constant_(self.lamb_mu, self.sigmoid(torch.tensor(-3)))
            init.constant_(self.lamb_sigma, self.sigmoid(torch.tensor(-3)))
            init.constant_(self.lamb_beta, self.sigmoid(torch.tensor(-5)))
            init.constant_(self.lamb_gamma, self.sigmoid(torch.tensor(-5)))
            if init_beta is None:
                init.constant_(self.bias_beta, 0.)
            else:
                self.bias_beta.copy_(init_beta)
            if init_gamma is None:
                init.constant_(self.bias_gamma, 1.)
            else:
                self.bias_gamma.copy_(init_gamma)
    
    def forward(self, x):

        b, c, _, _ = x.size()

        x_mean = torch.mean(x, dim=(2, 3))
        x_std = torch.sqrt(torch.var(x, dim=(2, 3)) + self.eps)
        
        # standardization
        x_stan_mean = self.stan_mean(self.stan_encoder(x_mean))
        x_stan_std = self.stan_std(self.stan_encoder(x_std))

        lamb_mu = self.sigmoid(self.lamb_mu)
        lamb_sigma = self.sigmoid(self.lamb_sigma)

        x_stan_mean = x_stan_mean * lamb_mu + x_mean * (1 - lamb_mu)
        x_stan_std = x_stan_std * lamb_sigma + x_std * (1 - lamb_sigma)

        x_stan_mean = x_stan_mean.reshape((b, c, 1, 1))
        x_stan_std = x_stan_std.reshape((b, c, 1, 1))

        x = (x - x_stan_mean) / x_stan_std

        # rescaling
        x_rsc_beta = self.rsc_beta(self.rsc_encoder(x_mean))
        x_rsc_gamma = self.rsc_gamma(self.rsc_encoder(x_std))

        x_rsc_beta = x_rsc_beta * self.lamb_beta + self.bias_beta
        x_rsc_gamma = x_rsc_gamma * self.lamb_gamma + self.bias_gamma

        x_rsc_beta = x_rsc_beta.reshape((b, c, 1, 1))
        x_rsc_gamma = x_rsc_gamma.reshape((b, c, 1, 1))

        x = x * x_rsc_beta + x_rsc_gamma

        return x

def set_module(model, name, module):
    """ Replace module of model by name with multi-level path """
    path = name.split(".")
    cur = model
    for p in path[:-1]:
        cur = getattr(cur, p)
    setattr(cur, path[-1], module)

def build_ASR_Norm(model: nn.Module, init=False):
    for name, module in model.named_modules():
        if isinstance(module, nn.BatchNorm2d):
            set_module(model, name, ASRNorm(module.num_features, init_beta=(module.weight if init else None), init_gamma=(module.bias if init else None)))
    
    return model

实验结果

考虑单源域在 PACS 上进行复现，即将其中一个域作为源域，另外三个域混合作为目标域，实验参数如下

学习率：0.001
优化器：SGD
epoch：50
batch size：32
lr scheduler：cosine 下降到初值的 0.1 倍

将上述代码模块添加到 RSC^[4] 的开源代码中，结果如下表所示

MethodDomain	art_painting	cartoon	photo	sketch	Avg
RSC	70.22	76.96	41.16	45.13
RSC(Paper)	73.4	75.9	41.6	56.2	61.8
RSC+ASR				52.27
RSC+ASR(Paper)	76.7	79.3	54.6	61.6	68.1
↑ to RSC
↑ to RSC(Paper)	3.3	3.4	5.4	13.0	6.3

Paper: 论文中报告的实验结果

下面的是多源域的结果

MethodDomain	art_painting	cartoon	photo	sketch	Avg
RSC	84.62*	82.28	98.83	72.61
RSC(Paper)	83.4	80.3	96.0	80.9	85.2
RSC+ASR	66.83*	77.22	94.74	76.89
RSC+ASR(Paper)	84.8	81.8	96.1	82.6	86.3
↑ to RSC
↑ to RSC(Paper)	1.4	1.5	0.1	1.7	1.1

Conclusion

作者提出了ASR-Norm，一种新颖的自适应和通用规范化形式，它使用自动编码器结构神经网络学习标准化和重新缩放统计量。ASR-Norm是一种通用算法，它通过使统计量适应不同域的数据来补充单域泛化的各种对抗域增强（ADA）方法，从而提高跨域的模型泛化能力，效果很好

References

如果对你有帮助的话，请给我点个赞吧~

欢迎前往我的博客查看更多笔记

1.A. Sinha, H. Namkoong, and J. Duchi. Certifying some distributional robustness with principled adversarial training. In International Conference on Learning Representations, 2018. ↩︎
2.S. Jia, D.-J. Chen, and H.-T. Chen. Instance-level meta normalization. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 4865–4873, 2019. ↩︎
3.R. Volpi, H. Namkoong, O. Sener, J. C. Duchi, V. Murino, and S. Savarese. Generalizing to unseen domains via adversarial data augmentation. In Advances in neural information processing systems, pages 5334–5344, 2018. ↩︎
4.RSC, ECCV, 2020: Self-challenging Improves Cross-Domain Generalization (论文笔记) ↩︎