小鲸鱼的梦境
0%

『论文笔记』Lipschitz Normalization for Self-Attention Layers with Application to Graph Neural Networks

发表于 更新于 分类于 Valine：
本文字数： 2.5k 阅读时长 ≈ 2 分钟

Information

  • Title: Lipschitz Normalization for Self-Attention Layers with Application to Graph Neural Networks
  • Author: George Dasoulas, Kevin Scaman, Aladin Virmaux
  • Institution: Noah’s Ark Lab, Huawei Technologies France
  • Year: 2021
  • Journal: ICML
  • Source: Arxiv, Github repository
  • Idea: 提出了 LipschitzNorm 来提高 GNN 模型性能，并利用 Lipschitz 连续性在理论上证明了方法的有效性
1
2
3
4
5
6
7
@inproceedings{inproceedings,
author = {Dasoulas, George and Scaman, Kevin and Virmaux, Aladin},
year = {2021},
month = {09},
pages = {},
title = {Lipschitz Normalization for Self-Attention Layers with Application to Graph Neural Networks}
}

该论文仅做略读

Abstract

通过对注意力分数进行 normalization 使深度注意力模型具有 Lipschitz 连续性能显著提高模型性能。

梯度爆炸现象使 GAT（图注意力网络）在基于梯度下降的训练算法中性能降低，为解决这一问题，作者引入 LipschitzNorm 方法来使得模型具有 Lipschitz 连续性。

Introduction

主要用于基于注意力的图神经网络，包括 GAT （graph attention networks) 和 GT (graph transformers)

除此之外，作者还展示了没有 norm 原始的注意力机制在这种结构中因为缺乏 Lipschitz 连续性会导致梯度爆炸。

Method

对 \(g(x) = W^TX\) 的正则化方法流程

norm_pipeline

对 Transformer 的 LipschitzNorm 包含三步：

  1. 计算查询 \(Q\) 的 F-范数 \(u = \sqrt{\sum_i \|q_i\|_2^2}\).
  2. 计算输入向量的最大2-范数 \(v=\max_i \|x_i\|_2\) (或 Transformer的 \(v=\max_i \|k_i\|_2\) 和 \(w=\max_i \|v_i\|_2\))
  3. 最后用 分数函数除以 \(uv\) (或 Transformer 的 \(\max\{uv, uw, vw\}\))

Detail

第 3 节给了一些定义，包括各种范数、Lipschitz 连续、注意力模型等

第 4 节说明了一个问题：注意力倾向于注意少数值，对少数值加权后会使得大的数更大导致梯度也更大。作者给出了注意力模型梯度范数的上界

第 5 节详细说明了作者提出的方法 LipschitzNorm

第 6 节指出模型 Lipschitz 常数的上界是每层 Lipschitz 常数的累积，所以经过一层层的累积导致了梯度爆炸

下图中左图展示了梯度爆炸的现象，右图展示了添加 Norm 后可以缓解梯度爆炸

att_grads_heatmap

下图说明梯度爆炸也会导致性能降低

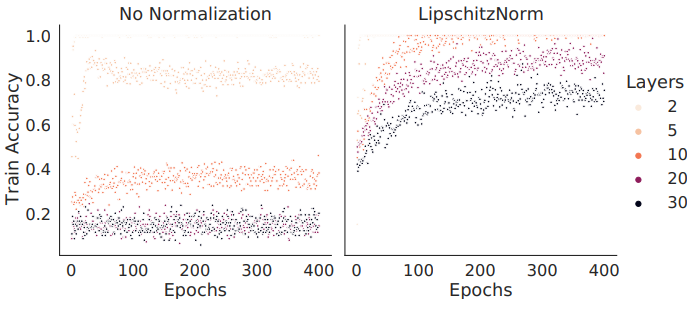
image-20220829151755843

Experiment

都是图网络的，就不看了

Conclusion

提出了 LipschitzNorm 的正则化方法，用于使自注意力层保持 Lipschitz 连续性，效果很好...

Others

代码实现

实话说这个 scatter 操作有点懵，没太懂是干什么的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
import torch, torch.nn as nn
from torch_scatter import scatter

class LipschitzNorm(nn.Module):
    def __init__(self, att_norm = 4, recenter = False, scale_individually = True, eps = 1e-12):
        super(LipschitzNorm, self).__init__()
        self.att_norm = att_norm
        self.eps = eps
        self.recenter = recenter
        self.scale_individually = scale_individually

    def forward(self, x, att, alpha, index):
        att_l, att_r = att
        
        if self.recenter:
            mean = scatter(src = x, index = index, dim=0, reduce='mean')
            x = x - mean


        norm_x = torch.norm(x, dim=-1) ** 2
        max_norm = scatter(src = norm_x, index = index, dim=0, reduce = 'max').view(-1,1)
        max_norm = torch.sqrt(max_norm[index] + norm_x)  # simulation of max_j ||x_j||^2 + ||x_i||^2

        
        # scaling_factor =  4 * norm_att , where att = [ att_l | att_r ]         
        if self.scale_individually == False:
            norm_att = self.att_norm * torch.norm(torch.cat((att_l, att_r), dim = -1))
        else:
            norm_att = self.att_norm * torch.norm(torch.cat((att_l, att_r), dim=-1), dim = -1)

        alpha = alpha / ( norm_att * max_norm + self.eps )
        return alpha

scatter 函数功能如下

add

References

如果对你有帮助的话，请给我点个赞吧~

欢迎前往 我的博客 查看更多笔记

--- ♥ end ♥ ---

欢迎关注我呀~