聚类算法

前言

因为在研究中有涉及到聚类算法，所以对传统的一些聚类算法进行了一些研究、总结、测试。

---

K-Mean

先了解了一些聚类的算法，然后手动实现了 K-Mean 聚类代码，在 visdom 上做了可视化测试，但结果却不是很好，经常出现分得很差的情况

K-Mean 聚类的基本思想如下：

1. 随机选择 \(K\) 个位置作为聚类中心（11.08 更新：随机选要估计范围，改为随机选 \(K\) 个点作为聚类中心
2. 遍历点集，将点集分配到距离最近的聚类中心所在的聚类中（这里的聚类采用欧氏距离）
3. 重新计算聚类中心，新的聚类中心是聚类中的点的均值（这里万一是空集要怎么处理？）
4. 重复 step.2 和 step.3 直到没有聚类不再变化

优点是算法简单，代价不大，缺点是容易陷入局部最小值，还得事先确定 \(K\) 的大小

import time, math, sys, os, re
from typing import List
import torch
import numpy as np
import random
from util import *

def Product_dots(n: int, m: int, r: int, s: int, left: int = -100, right: int = 100):
    """n 个中心，每个中心产生距离不超过 r 的 m 个随机点，每两个中心的距离不小于 s，中心的范围在 [left, right] 之间"""
    center = list()
    for i in range(n):
        while True:
            x, y = random.randint(left, right), random.randint(left, right)
            for i, j in center:
                if (x - i) ** 2 + (y - j) ** 2 < s * s:
                    break
            else:
                center.append([x, y])
                break
    dots = list()
    for x, y in center:
        for i in range(m):
            dots.append([x + random.uniform(-1, 1) * r, y + random.uniform(-1, 1) * r])
    return center, dots

def distance(x, y, i, j):
    return (x - i) ** 2 + (y - j) ** 2

def k_means(k: int, dots: List[List], center=None) -> List:
    """将点集分为 k 类, center 仅供测试使用"""
    s = [[] for _ in range(k)]
    if not center:
        center = [[random.randint(-100, 100), random.randint(-100, 100)] for _ in range(k)]

    vis = defaultdict(int)

    while True:
        changed = False
        s = [list() for _ in range(k)]
        # 计算每个点到所有中心中最近的那个的，分配到那个簇
        for x, y in dots:
            ind, dist = 0, float('inf')
            for i, (a, b) in enumerate(center):
                d = distance(x, y, a, b)
                if d < dist:
                    ind, dist = i, d
            s[ind].append([x, y])
            if not ind == vis[str(x) + '_' + str(y)]:
                changed = True
                vis[str(x) + '_' + str(y)] = ind
        # 重新计算中心
        center = [[sum(a for a, _ in t) / len(t), sum(b for _, b in t) / len(t)] if t else [random.randint(-100, 100), random.randint(-100, 100)] for t in s]
        if not changed:
            break

    return center, s
            

if __name__ == '__main__':
    center, dots = Product_dots(10, 50, 5, 20)
    plotter = VisdomPlotter()
    color = np.array([255,255,255],ndmin=2)
    # for x, y in center:
    #     plotter.plot_scatter(np.array([x, y], ndmin=2), None, 'x', 'y', 'K-Mean', 'center', win='before')
    # for x, y in dots:
    #     plotter.plot_scatter(np.array([x, y], ndmin=2), legend='dots', win='before')

    c, s = k_means(10, dots)
    for x, y in center:
        plotter.plot_scatter(np.array([x, y], ndmin=2), None, 'x', 'y', 'K-Mean-class', 'center', win='after', color=color)
    for i, t in enumerate(s, start=1):
        for x, y in t:
            plotter.plot_scatter(np.array([x, y], ndmin=2), legend='type-' + str(i), win='after')

    c, s = k_means(10, dots, center)
    for x, y in center:
        plotter.plot_scatter(np.array([x, y], ndmin=2), None, 'x', 'y', 'K-Mean-对照', 'center', win='对照', color=color)
    for i, t in enumerate(s, start=1):
        for x, y in t:
            plotter.plot_scatter(np.array([x, y], ndmin=2), legend='type-' + str(i), win='对照')

---

K-Mean++

然后继续对聚类的算法进行了一些研究，主要还是对 K-Mean 的一些改进方法，包括 bi-K-Mean, K-Mean++。

K-Mean++ 是对 K-Mean 算法的第一步进行了改进，由于一个合理的初始聚类中心对结果有很大影响（K-Mean 对初始敏感），根据聚类中心尽可能相互远离的原理，对 K-Mean 选取中聚类中心指定了一种策略，具体思路如下：

1. 先随机选择一个点作为聚类中心
2. 计算剩下所有点与聚类中心的最小聚类（多个聚类中心只记录最近那个的距离）
3. 根据上一步的距离设置概率（这里我觉得时候使用 softmax 函数）
4. 使用轮盘法选一个点作为聚类中心（可以理解为按概率大小随机选一个点）（为什么不直接选最远的呢，其实不难找到反例证明贪心是不正确的，但找最优解代价太大，折中下使用轮盘法随机选择）
5. 重复 step.2 ~ 4 直到有 \(K\) 个聚类中心

实践发现效果相当好，很多情况下甚至比 Bi-K-Mean 结果更好

def distance(x, y):
    """欧式距离（不开方）"""
    d = x - y
    return np.sum(d * d)

def k_means(dots: List[List], k: int, center=None) -> List:
    """将点集分为 k 类, numpy 版本，即点集是 n 维向量"""
    if len(dots) <= k:
        return [[i] for i in dots] + [[] for _ in range(k - len(dots))]

    s = None
    # 计算聚类中心
    if not center:
        # 随机选一个作为聚类中心
        center = [dots[random.randint(0, len(dots) - 1)]]
        # 轮盘法选 k - 1 个点
        for _ in range(k - 1):
            dist = [min(math.sqrt(distance(x, c)) for c in center) for x in dots]
            pro_dist = [math.exp(x) for x in dist]
            sum_dist = sum(pro_dist)
            pro_dist = [x / sum_dist for x in pro_dist]
            select_dist = list(itertools.accumulate(pro_dist))
            rnum = random.random()
            for i, j in enumerate(select_dist):
                if j > rnum:
                    rnum = i
                    break
            center.append(dots[i])

    vis = [0 for _ in dots]

    while True:
        changed = False
        s = [list() for _ in range(k)]
        # 计算每个点到所有中心中最近的那个的，分配到那个簇
        for j, x in enumerate(dots):
            ind, dist = 0, float('inf')
            for i, y in enumerate(center):
                d = distance(x, y)
                if d < dist:
                    ind, dist = i, d
            s[ind].append(x)
            if not ind == vis[j]:
                changed = True
                vis[j] = ind
        # 重新计算中心
        center = [sum(t) / len(t) if t else np.random.random(size=dots[0].shape) for t in s]
        if not changed:
            break

    return center, s

重写的方法基于 numpy 实现，这样后续如果要改为基于 Pytorch 实现也会很容易

Bi-K-Mean 是二分实现的 K-Mean，基本思路是：

1. 选一个点作为聚类中心（或者说整个点集作为一个聚类）
2. 尝试将每个点集使用 K-Mean 一分为二，即 \(K=2\) 的 K-Mean 算法
3. 计算损失 SSE ，对损失最小的聚类进行拆分
4. 重复上面两步直到满 \(K\) 个聚类

def SequaredError(dots):
    """计算一簇聚类的 SSE"""
    if not dots:
        return 0
    center = sum(dots) / len(dots)
    return np.sum(sum((dot - center) ** 2 for dot in dots))

def Bi_K_means(dots, k):
    # 视为一个簇
    s = [dots]
    while len(s) < k:
        c, p, ind = float('inf'), None, -1
        # 对每个簇，计算一分为二的 SSE 改变值，选最小的作为新的簇
        for i, dot in enumerate(s):
            old_sse = SequaredError(dot)
            _, p2 = k_means(dot, 2)
            new_sse = sum(SequaredError(d) for d in p2)
            if new_sse - old_sse < c:
                c, p, ind = new_sse - old_sse, p2, i
        tmp = list()
        for i, dot in enumerate(s):
            if i == ind:
                tmp.extend(p)
            else:
                tmp.append(dot)
        s = tmp
        
    return s

网上的介绍所这种方法得到的结果是全局最优解，但测试以后发现并不是 ，因为将聚类拆分上是用了贪心的思想，容易证明这只是局部最优而非全局最优，实验中也发现很多时候该方法得到的损失和比 K-Mean++ 的损失还要大，但相对而言优于 K-Mean

随机生成聚类中心和点集的测试结果如图所示，K-Mean++ 效果与初始聚类一样，而 Bi-K-Mean 结果却相对较差

正态分布散点聚类结果如下图

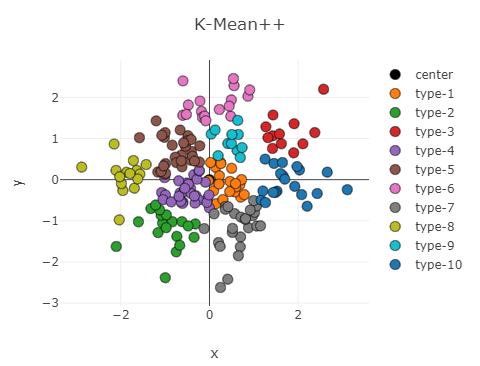
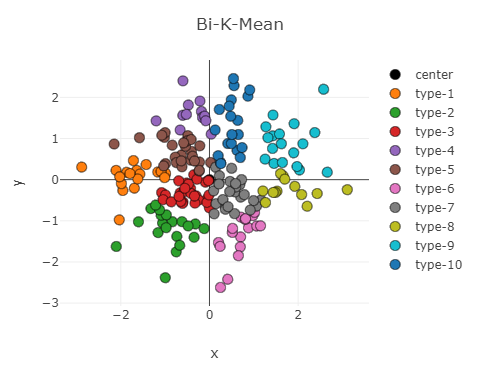
计算聚类中点到聚类中心聚类的平方和为：

K-Mean = 53.31382575076519
Bi_KMEAN = 59.136002328973206

显然 Bi-K-Mean 的效果还不如 K-Mean++

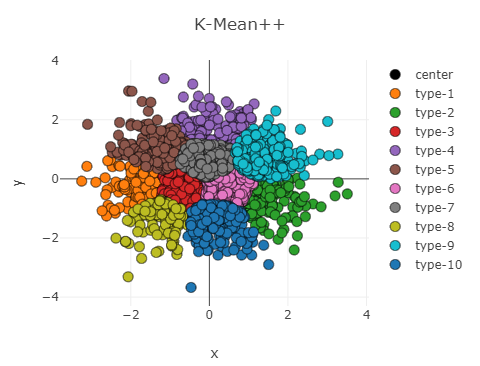
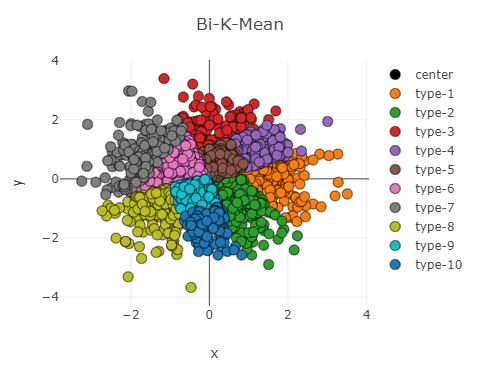
在高密度的点集下，可以明显看到 Bi-K-Mean 的聚类间边界分明成直线，而 K-Mean++ 的边界就自然得多，并且从 SSE 上看也是 K-Mean++ 的效果更好

K-Mean = 658.3800952519407
Bi_KMEAN = 774.3682173208291

K-Mean++矩阵实现形式

对 K-Mean++ 的代码进行了改造，使其能运行在输入为一个 \(n \times m\) 的矩阵上进行聚类（2021.11.11 返回值中增加了索引）

def distance(x, y):
    """欧式距离（不开方）"""
    d = x - y
    return torch.sum(d * d)

def k_means(dots, k: int) -> List:
    """K-Mean++ 聚类 (提醒，数据要先做归一化处理避免在调用 softmax 函数时 math.exp 溢出错误, exp(507) 开始就会溢出)

    Args:
        dots (tensor): 一个 n x m 的矩阵，表示 n 个 m 维的向量进行聚类
        k (int): 聚类的数量

    Returns:
        List[tensor]: k 个一维的中心点，k 个 s_k x m 的矩阵 (s_k 表示聚类中的向量数量)，dots 中的每个点属于哪个聚类
    """
    n, m = dots.size()
    if n <= k:
        return [dots[i].unsqueeze(0) for i in range(n)] + [torch.tensor([[]]) for _ in range(k - n)]

    s = None
    # 计算聚类中心
    # 随机选一个点作为聚类中心
    center = [dots[random.randint(0, n - 1)]]
    # 再用轮盘法选 k - 1 个点
    for _ in range(k - 1):
        dist = [min(math.sqrt(distance(dots[i], c)) for c in center) for i in range(n)]
        pro_dist = [math.exp(x) for x in dist]
        sum_dist = sum(pro_dist)
        pro_dist = [x / sum_dist for x in pro_dist]
        select_dist = list(accumulate(pro_dist))
        rnum = random.random()
        for i, j in enumerate(select_dist):
            if j > rnum:
                rnum = i
                break
        center.append(dots[rnum])

    vis = [0 for _ in range(n)]

    while True:
        changed = False
        s = [list() for _ in range(k)]
        # 计算每个点到所有中心中最近的那个的，分配到那个簇
        for j in range(n):
            ind, dist = 0, float('inf')
            for i, y in enumerate(center):
                d = distance(dots[j], y)
                if d < dist:
                    ind, dist = i, d
            s[ind].append(dots[j])
            if not ind == vis[j]:
                changed = True
                vis[j] = ind
        # 重新计算中心
        center = [sum(t) / len(t) if t else dots[random.randint(0, n - 1)] for t in s]
        if not changed:
            break
    
    return center, [torch.stack(t) for t in s], vis

测试代码如下：

if __name__ == '__main__':
    x = torch.randn(size=(5000, 2))
    center, s = k_means(x, 10)
    plotter = VisdomPlotter()

    for i, d in enumerate(s):
        plotter.plot_scatter(d, xlabel='x', ylabel='y', title='Pytorch-K-Mean', legend='type-' + str(i), win='Pytorch-K-Mean')

测试结果：

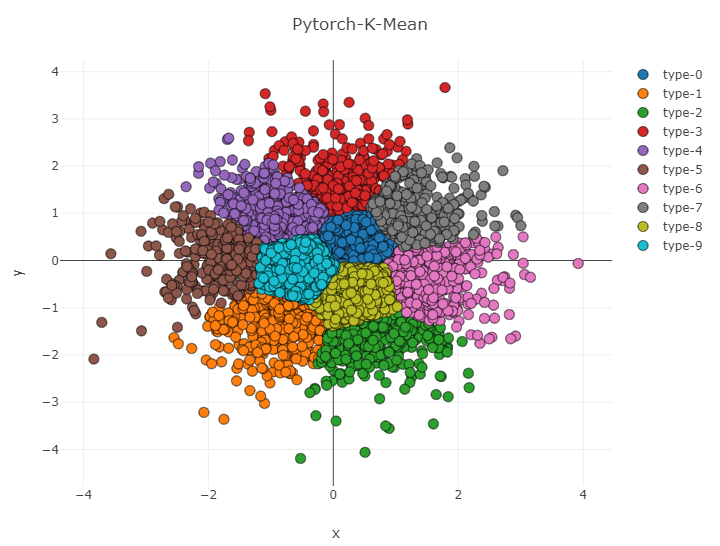
显示了相对满意的聚类结果

接下来考虑的是在网络的实现过程中如何确定聚类的数目

---

DBSCAN聚类算法

DBSCAN 是一种基于密度的算法，基本想法是一定范围内的点都归到一个聚类，并且范围内的点可以继续拓展该聚类

有两个参数 \(\varepsilon\) 和 \(minPts\) ，分别表示邻域范围和形成高密度区域所需最少点数，伪代码如下

DBSCAN(D, eps, MinPts) {
   C = 0
   for each point P in dataset D {
      if P is visited
         continue next point
      mark P as visited
      NeighborPts = regionQuery(P, eps)
      if sizeof(NeighborPts) < MinPts
         mark P as NOISE
      else {
         C = next cluster
         expandCluster(P, NeighborPts, C, eps, MinPts)
      }
   }
}

expandCluster(P, NeighborPts, C, eps, MinPts) {
   add P to cluster C
   for each point P' in NeighborPts { 
      if P' is not visited {
         mark P' as visited
         NeighborPts' = regionQuery(P', eps)
         if sizeof(NeighborPts') >= MinPts
            NeighborPts = NeighborPts joined with NeighborPts'
      }
      if P' is not yet member of any cluster
         add P' to cluster C
   }
}

regionQuery(P, eps)
   return all points within P's eps-neighborhood (including P)

所有点被分成三类：核心点（\(\varepsilon\)-邻域范围内范围内有至少 \(minPts\) 个点）、可达点（在核心点 \(\varepsilon\)-邻域 范围内但不是核心点）、局外点（除了前两种以外的点）

基本步骤：

1. 点集中找到一个未被访问的点，检查是否是核心点，不是的话跳过，是的话建立一个新的聚类
2. 将 \(\varepsilon\)-邻域内的点都加入到该聚类
3. 对 聚类中的点，将其 \(\varepsilon\)-邻域内的点都加入聚类，直到聚类不再加点，这就是一个完整的聚类了
4. 重复上述步骤找到所以聚类，剩下的点是杂点

---

基于sklearn实现

使用二维数据便于可视化

创建数据集

import torch
import matplotlib.pyplot as plt
import sklearn.cluster as cluster
import random
import math

plt.figure(figsize=(100, 100))

使用二维数据，\(\text{size} = (n_{\text{sample}}, n_{\text{features}})\)，\(n\) 是样本数量, 数据范围 \([0, 100]\).

# 生成 点簇 数据
cnt_centers = 10        # 数据中心的数量
cnt_each_centers = 20   # 数据点的周围点的数量
size = 15

点簇数据生成

# 生成样本中心
centers = list()
centers_min_dist = (2 * size) ** 2
for _ in range(cnt_centers):
    while True:
        x, y = random.random() * 100, random.random() * 100
        if all((x - i) ** 2 + (y - j) ** 2 > centers_min_dist for i, j in centers):
            break
    centers.append((x, y))

# 生成样本
dots_list = list()
for x, y in centers:
    for _ in range(cnt_each_centers):
        dx, dy = random.random() * size, random.random() * size
        dots_list.append((x + dx, y + dy))

random.shuffle(dots_list)
dots = torch.tensor(dots_list)
print(dots.size())

随机数据生成

# 随机数据点
dots = torch.randn((50, 2))
print(dots.size())

环形数据簇

# 环形数据簇(3 个圆环)
cnt_centers = 3         # 数据中心的数量
cnt_each_centers = 5   # 数据点的周围点的数量
size = 10
center_x, center_y = 50, 50
dots_list = list()
for r, sample in zip([33, 66, 99], [32, 64, 96]):
    for i in range(sample):
        x, y = r * math.cos(2 * i * math.pi / (sample - 1)), r * math.sin(2 * i * math.pi / (sample - 1))
        for _ in range(cnt_each_centers):
            dx, dy = random.random() * size, random.random() * size
            dots_list.append((x + dx, y + dy))

random.shuffle(dots_list)
dots = torch.tensor(dots_list)
print(dots.size())

螺旋数据簇（2簇）

实际上是两条阿基米德螺线，即 \(r= 10 \theta\).

# 螺旋数据簇 （2 簇）
cnt_centers = 2         # 分类数
cnt_each_centers = 120  # 采样数量
sample = 5              # 采样点数
size = 8
dots_list = list()
st, ed, cy = 10, 100, 2.1 * 2 * math.pi        # 起始半径 10, 两圈后半径为100
r_step = (ed - st) / cnt_each_centers
c_step = cy / cnt_each_centers
for start in [0, math.pi]:
    r, t = st, start
    for i in range(cnt_each_centers):
        x, y = r * math.cos(t), r * math.sin(t)
        r += r_step
        t += c_step
        for _ in range(sample):
            dx, dy = random.random() * size, random.random() * size
            dots_list.append((x + dx, y + dy))

random.shuffle(dots_list)
dots = torch.tensor(dots_list)
print(dots.size())

绘图

# 生成色卡(彩虹渐变色)
#    红   橙   黄    绿   青    蓝   紫
# r: 255, 255, 255, 0  , 0  , 0  , 139
# g: 0  , 165, 255, 255, 255, 0  , 0
# b: 0  , 0  , 0  , 0  , 255, 255, 255
color = list()
color_step = (cnt_centers - 1) / 6

def mid(left, right, cur, l_color, r_color):
    if l_color < r_color:
        return int(l_color + (cur - left) * (r_color - l_color) / (right - left))
    else:
        return int((right - cur) * (l_color - r_color) / (right - left))

for i in range(cnt_centers):
    idx = int(i // color_step)
    if idx == 0:
        r, g, b = 255, mid(0, color_step, i, 0, 165), 0
    elif idx == 1:
        r, g, b = 255, mid(color_step, color_step * 2, i, 165, 255), 0
    elif idx == 2:
        r, g, b = mid(color_step * 2, color_step * 3, i, 255, 0), 255, 0
    elif idx == 3:
        r, g, b = 0, 255, mid(color_step * 3, color_step * 4, i, 0, 255)
    elif idx == 4:
        r, g, b = 0, mid(color_step * 4, color_step * 5, i, 255, 0), 255
    elif idx == 5:
        r, g, b = mid(color_step * 5, cnt_centers, i, 0, 139), 0, 255
    else:
        r, g, b = 139, 0, 255
    color.append("#{:0^2}{:0^2}{:0^2}".format(*map((lambda x: x[2:]), map(hex, (r, g, b)))))
print(color)

# 绘制原图
plt.figure(figsize=(4, 4), dpi=240)
plt.scatter(dots[:,0], dots[:,1], c='#8b00ff')
plt.title("Befort")
plt.savefig(f"1_{tag}_before.png", dpi=240)
plt.show()

---

K-Means

其实是 K-Mean++，不过也只是初始化方法不同而已

# 先试试 K-Means
label = cluster.KMeans(cnt_centers, ).fit_predict(dots)
dots_cls = [color[lab] for lab in label]
plt.figure(figsize=(4, 4), dpi=240)
plt.scatter(dots[:,0], dots[:,1], c=dots_cls)
plt.title("After")
plt.savefig(f"2_{tag}_after.png", dpi=240)
plt.show()

结果是这样的

点簇（稀疏）

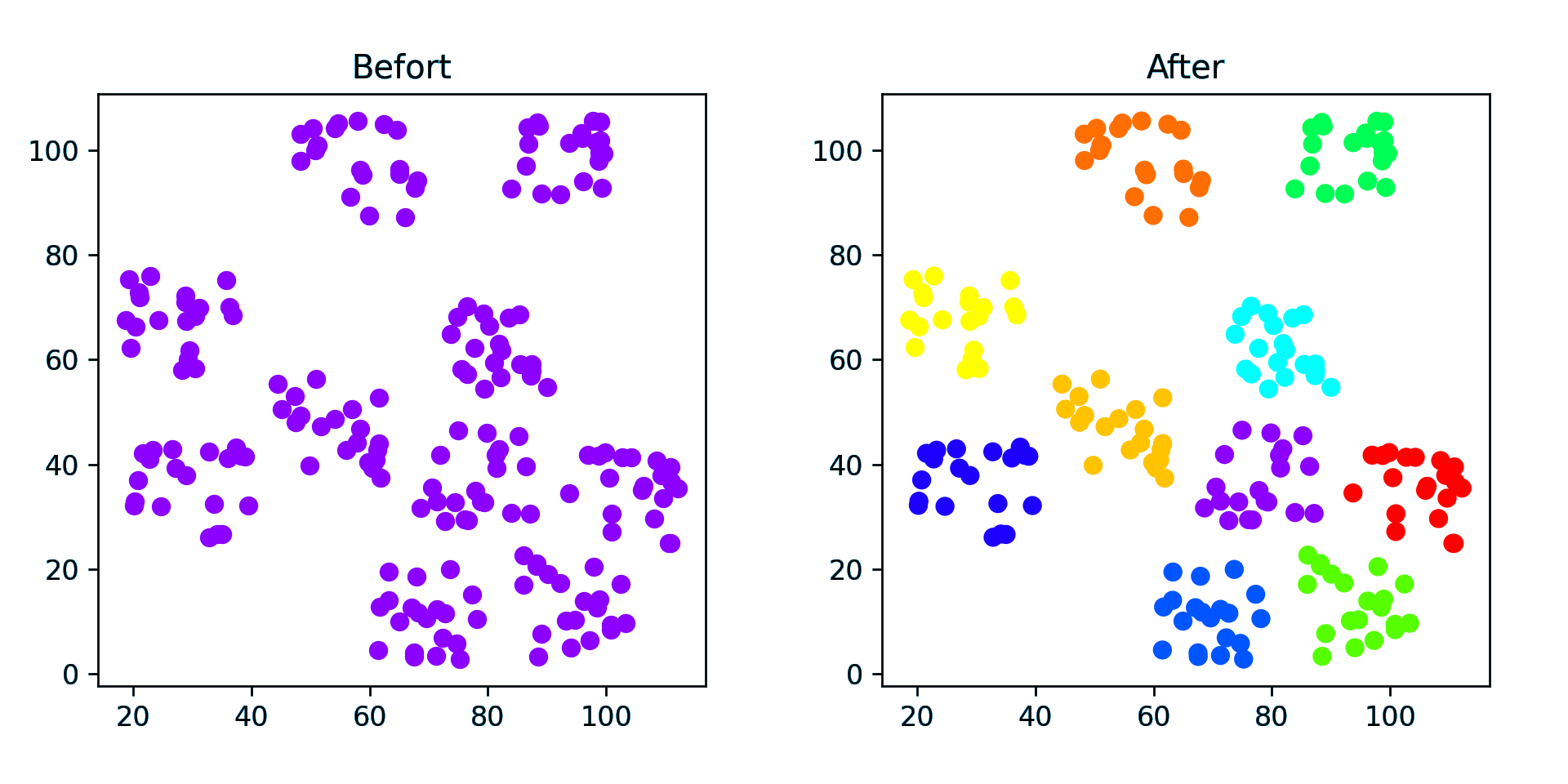
点簇（密集）

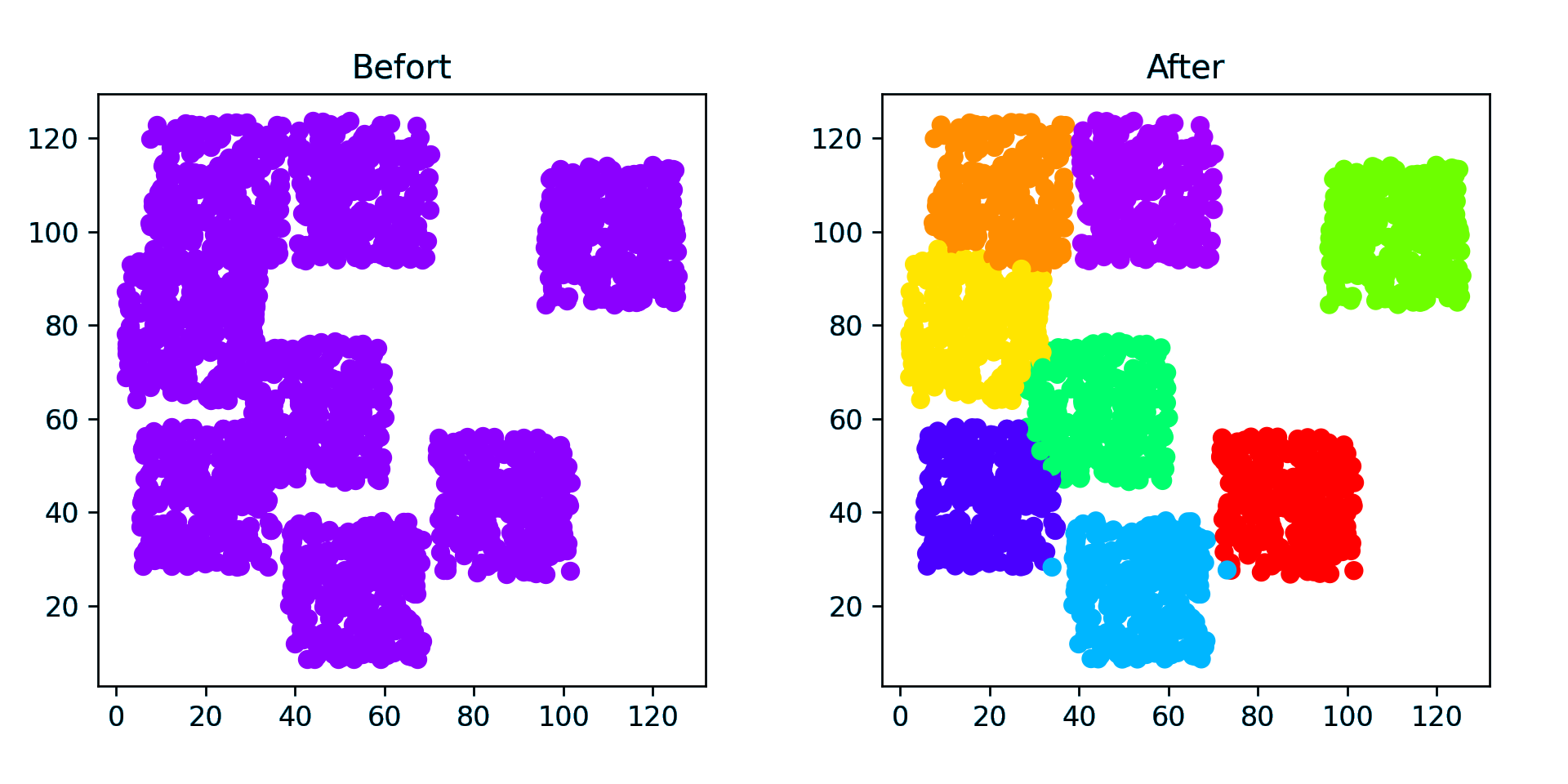
随机（稀疏） - 50 个点

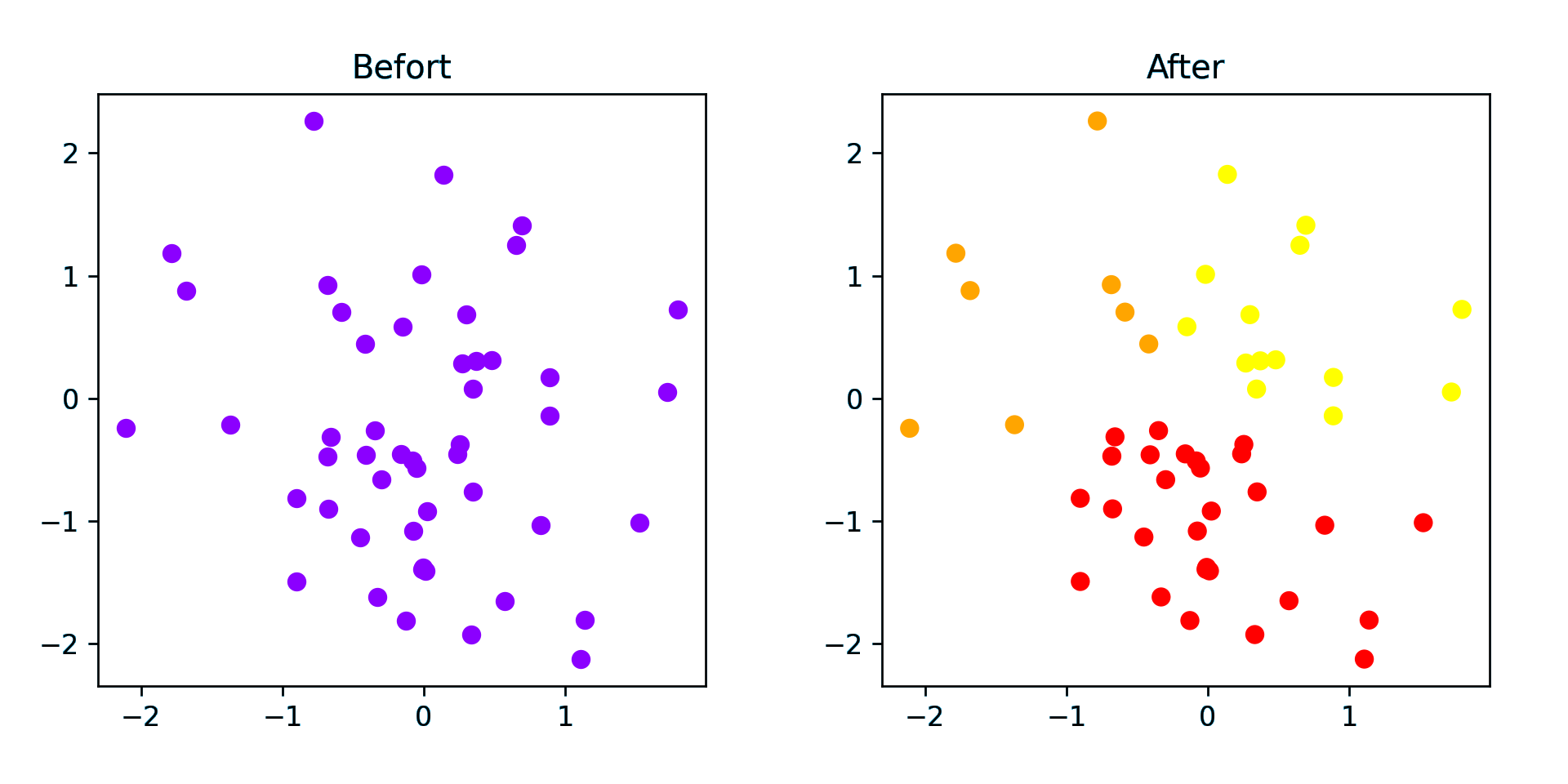
随机（密集） - 5000 个点（仅运行 1.8 s）

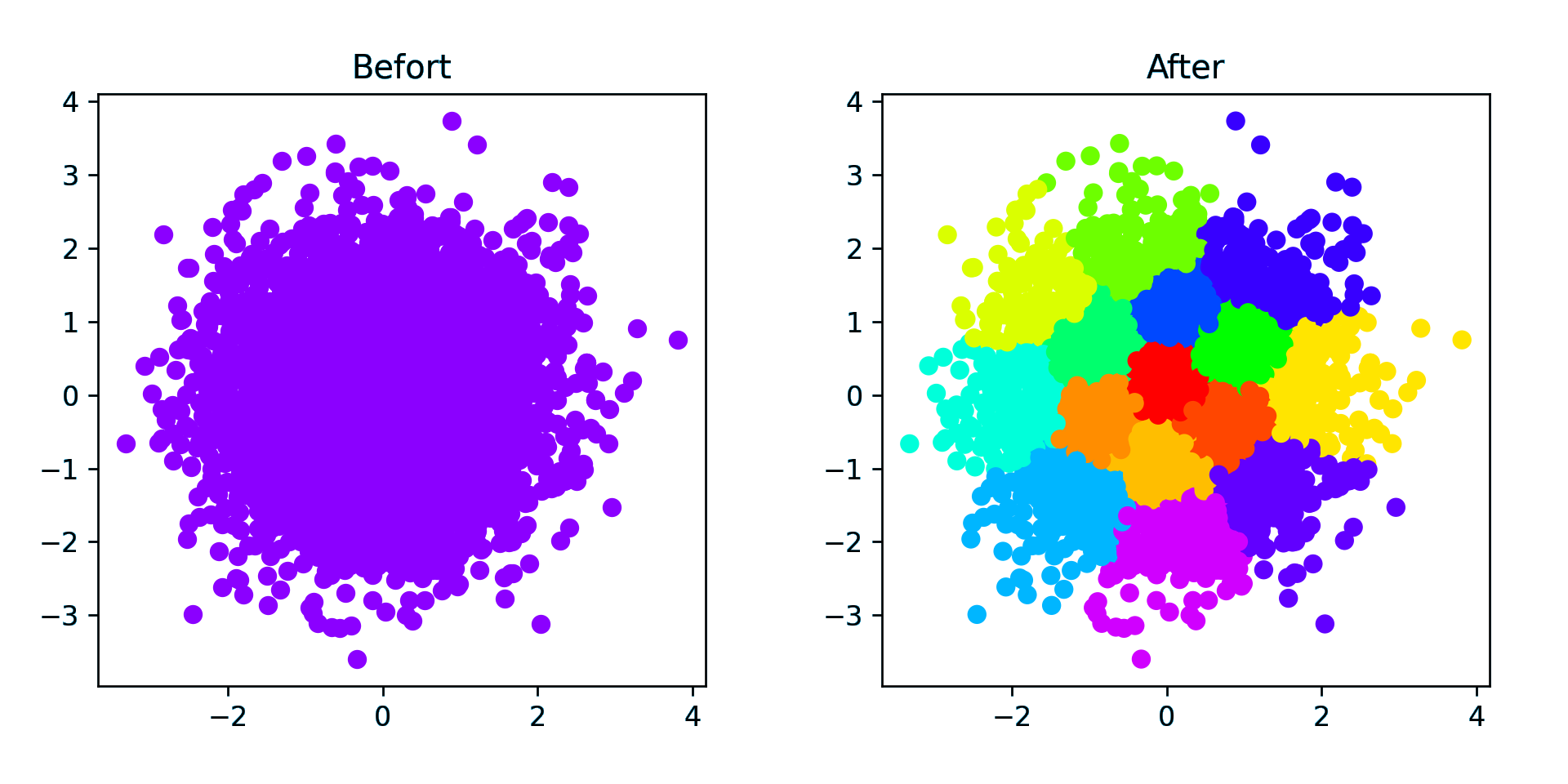
环形数据簇

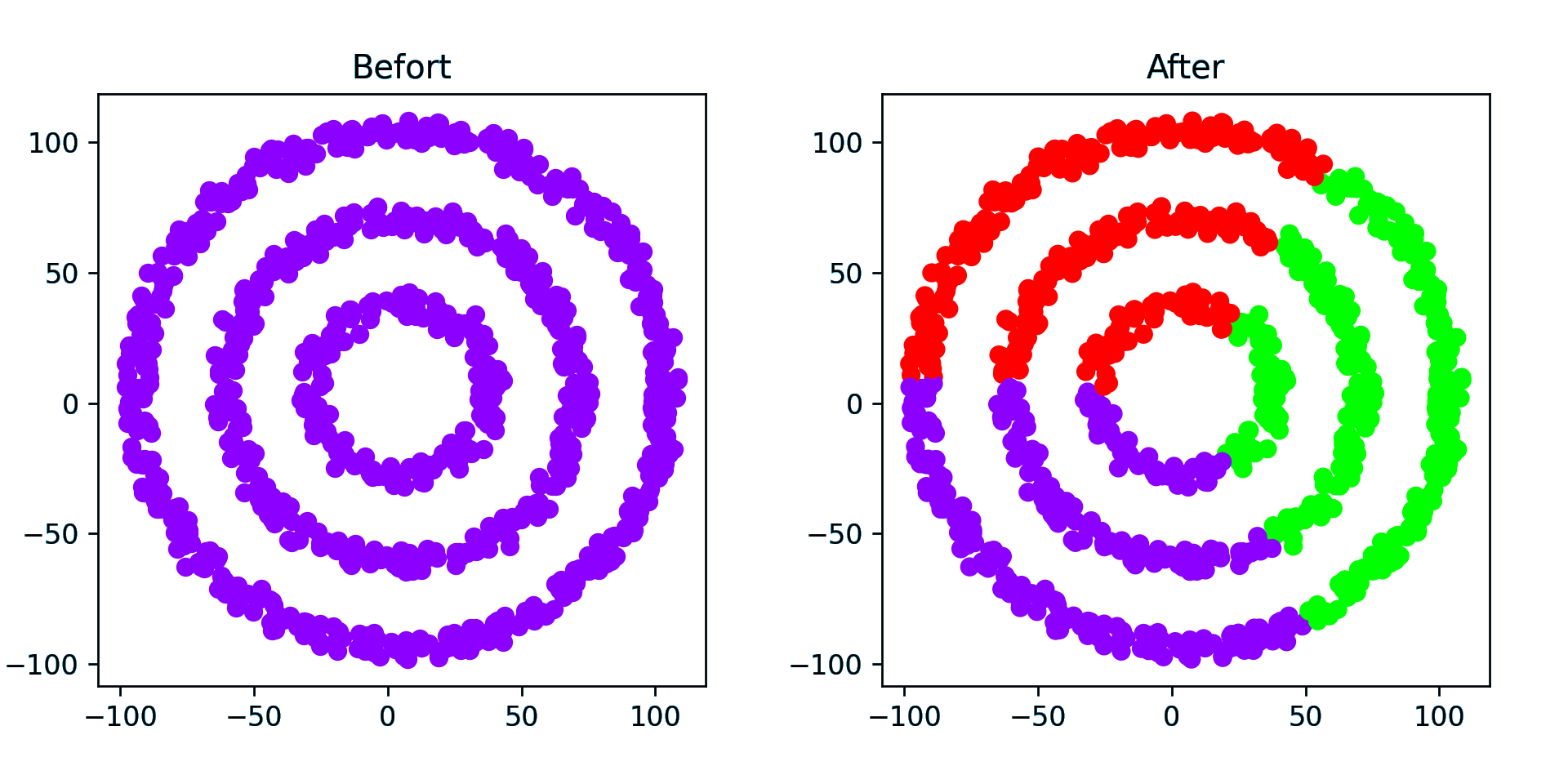
螺旋数据簇

---

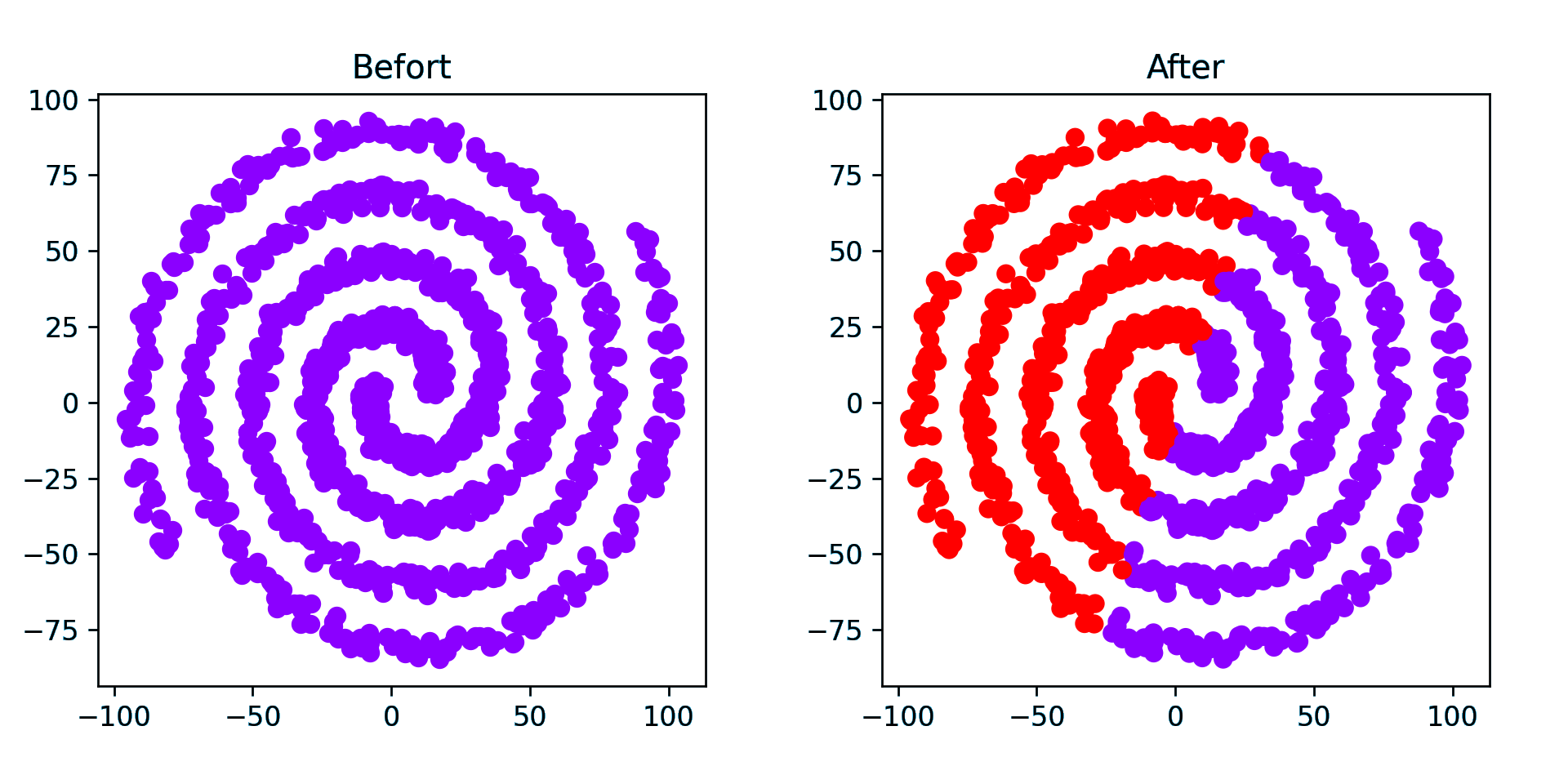
DBSCAN

label = cluster.DBSCAN(8, min_samples=3).fit_predict(dots)
label = list(lab for lab in label)
cnt_centers = max(label) + 2

因为是动态决定聚类数量的，所以运行聚类算法后才知道聚类数量，所以这里插入前面生成色卡的代码

dots_cls = [color[lab] for lab in label]
plt.figure(figsize=(4, 4), dpi=240)
plt.scatter(dots[:,0], dots[:,1], c=dots_cls)
plt.title("After")
plt.savefig(f"2_{tag}_after.png", dpi=240)
plt.show()

注意：下图中紫色可能为异常数据（如果有异常数据的话），分类中标签为 -1

螺旋数据簇

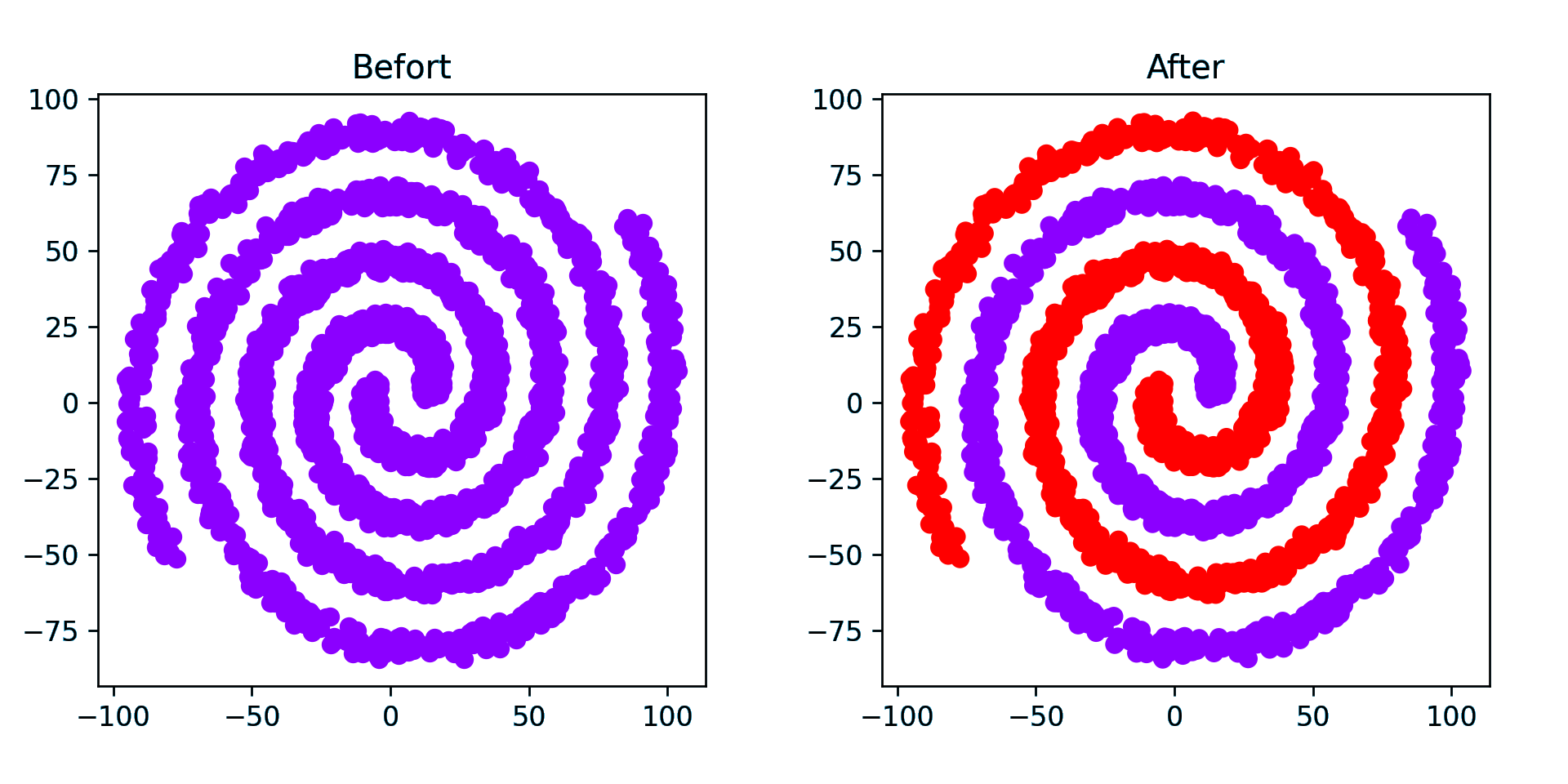
点簇

创建了 15 个聚类中心点，计算结果只有 8 个

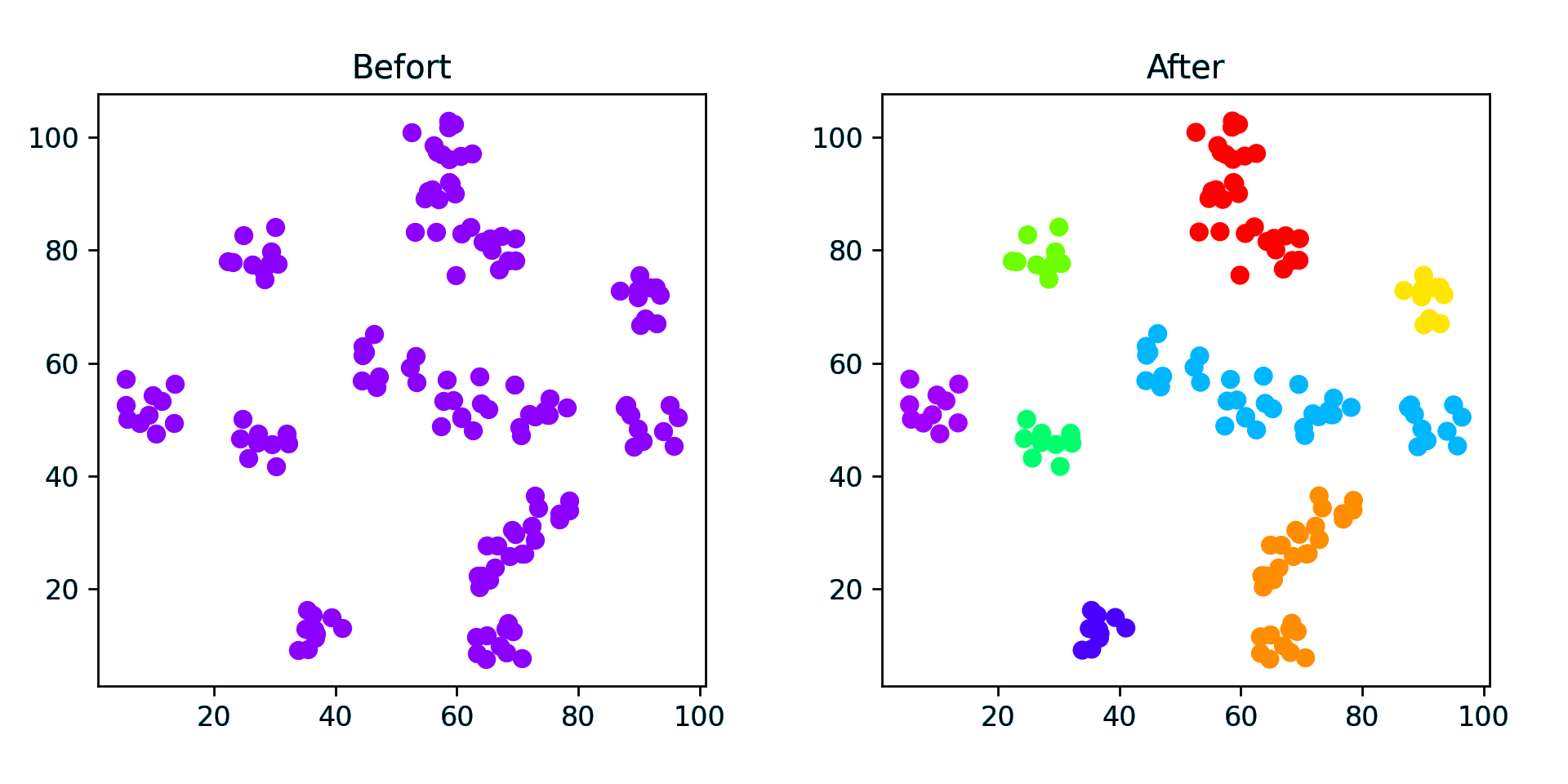
点簇（密集）

eps 为 3 才能分出 5 个类，为 5 的时候只有两类，更大则只有一类

注意到 5 类中间有一个异常点

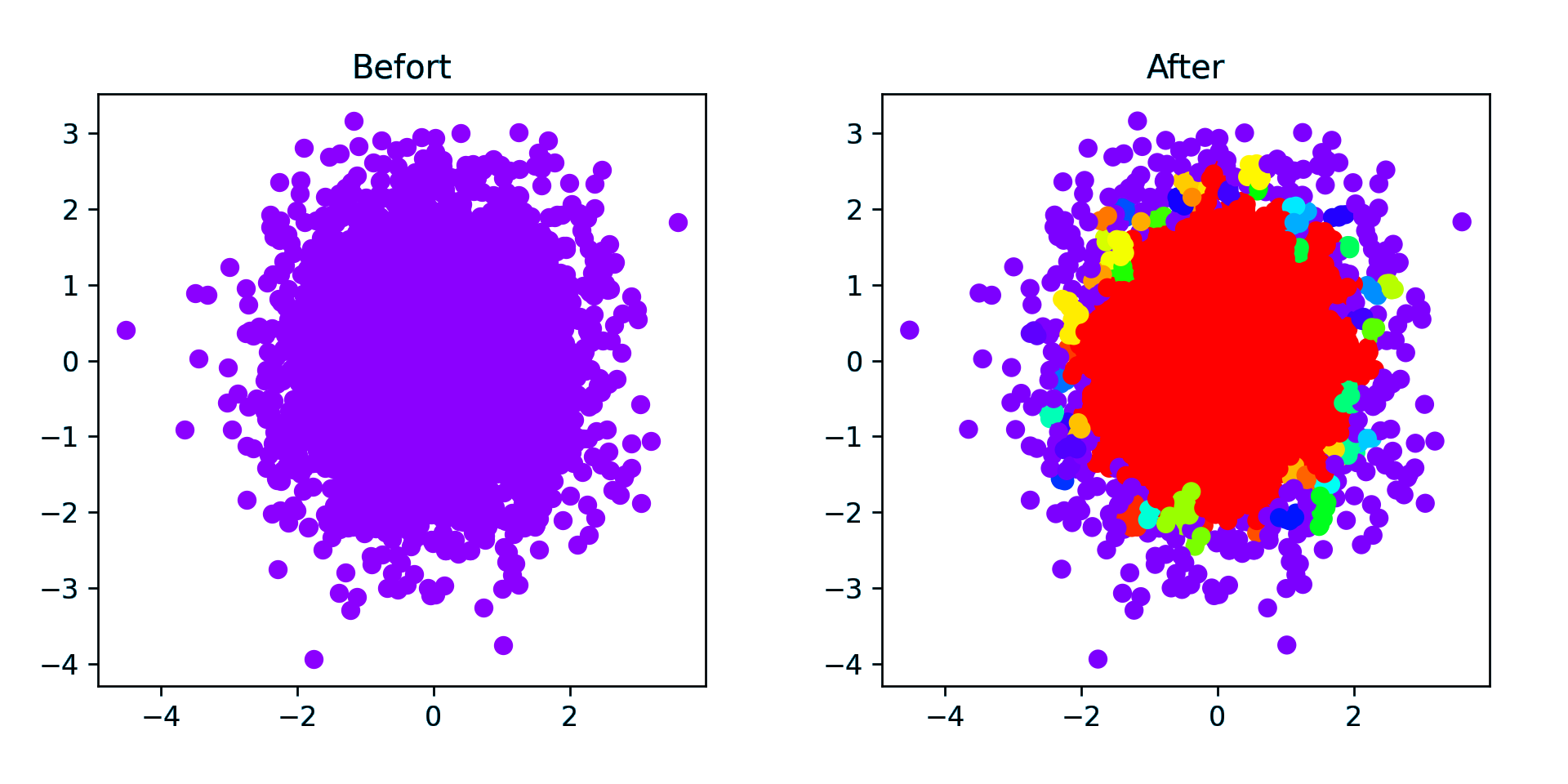
随机点（密集）

对于随机点 DBSCAN 效果并不好，因为 eps 难以确定

eps 为 0.5 的结果中只分了一类，剩下的都是异常点

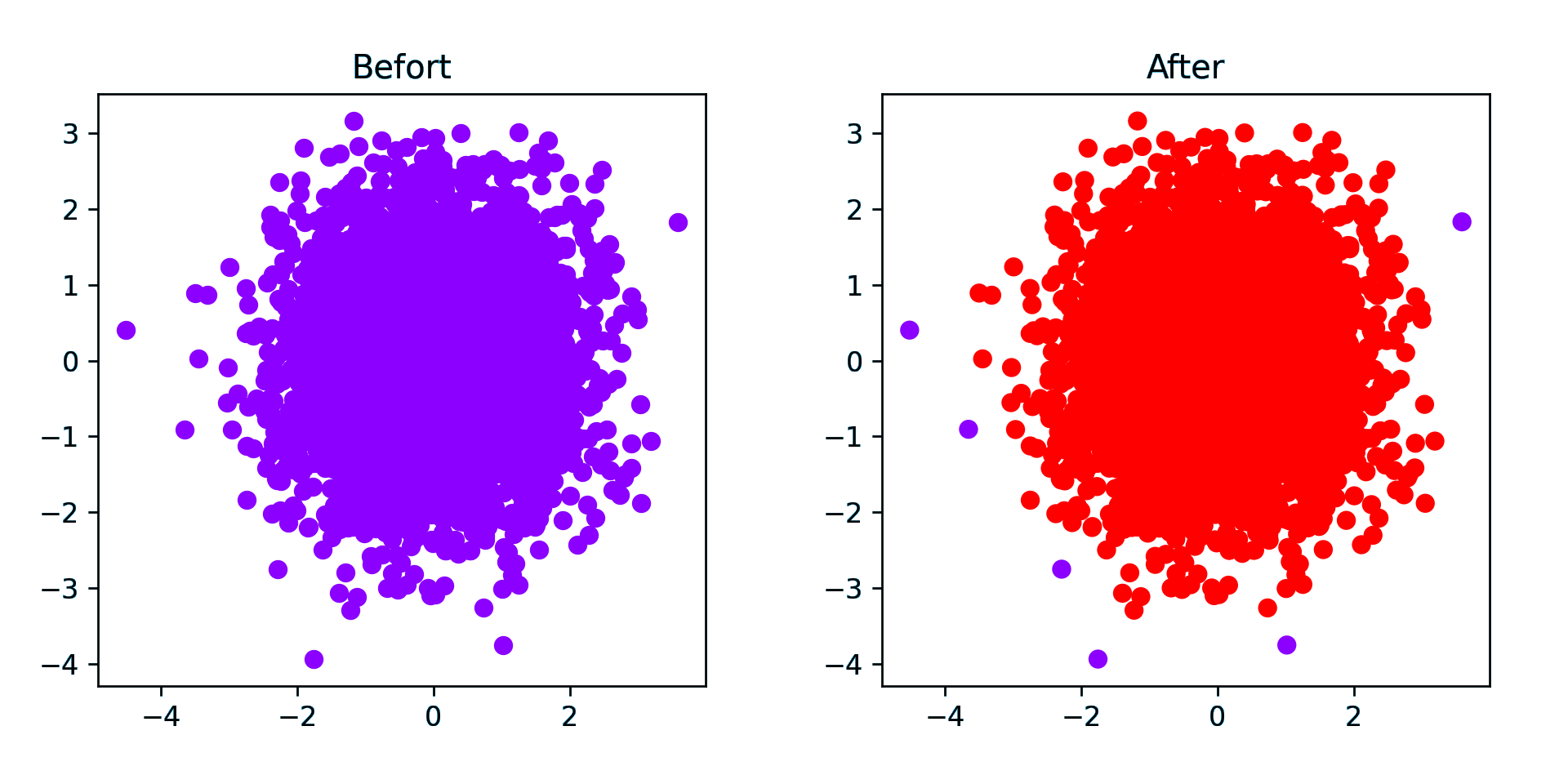
eps 为 0.1 则分出了 50 类，是一个失败的聚类，中间的大量分在一类而外围有大量异常点，所以说 DBSCAN 不适合随机情况的聚类

环形点簇

eps 设为 10 比较合理，太小就不止 3 类了

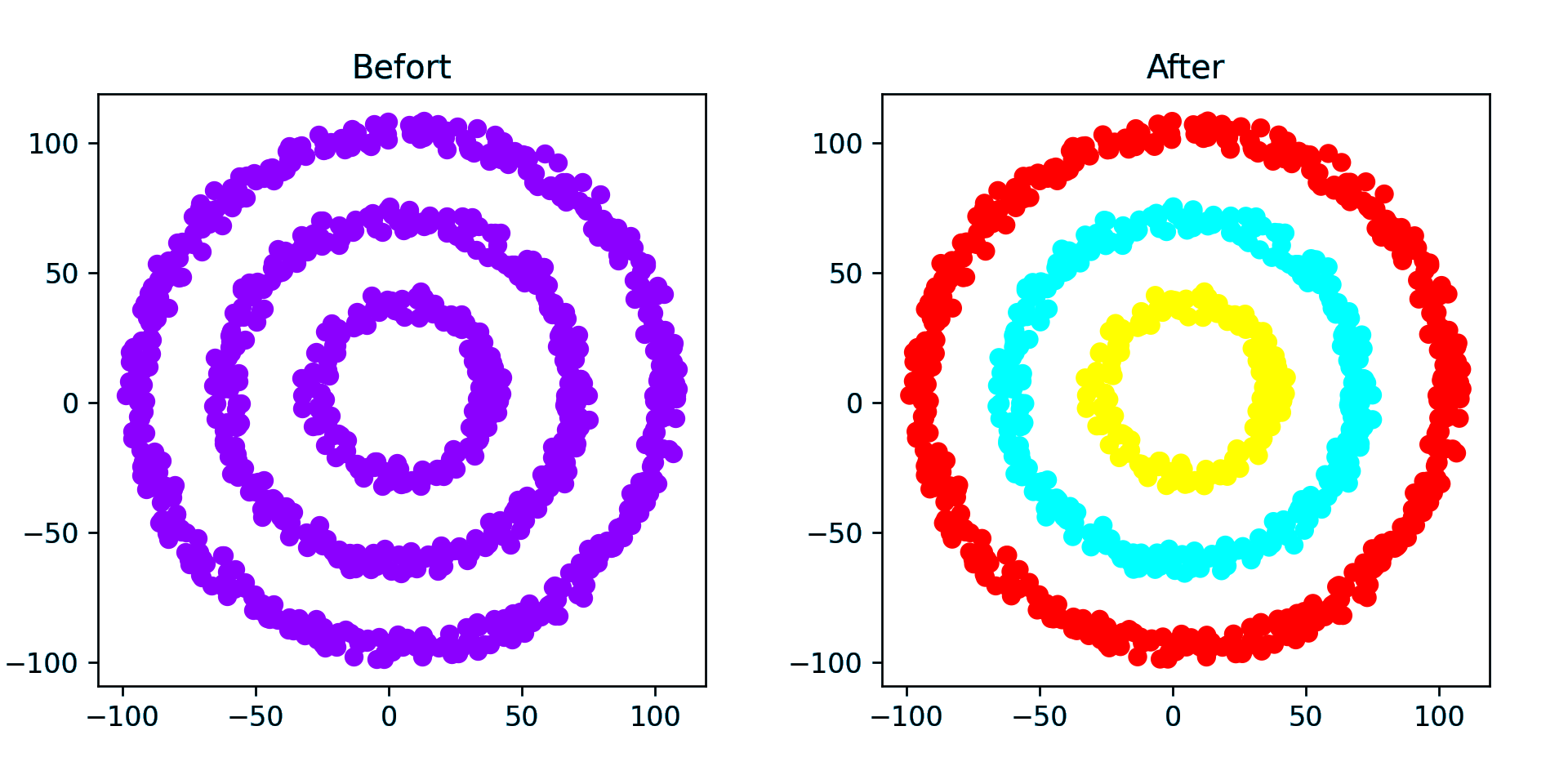
总结：显然，DBSCAN 更擅长中心距离比较大的情况，对于随机点效果非常差，除此之外的另外一个问题就是参数 eps 不太容易处理

---

谱聚类

在 scikit-learn 的类库中，sklearn.cluster.SpectralClustering实现了基于 Ncut 的谱聚类，没有实现基于 RatioCut 的切图聚类。同时，对于相似矩阵的建立，也只是实现了基于 K 邻近法和全连接法的方式，没有基于 \(\epsilon\) -邻近法的相似矩阵。最后一步的聚类方法则提供了两种，K-Mean s算法和 discretize 算法。

对于SpectralClustering的参数，我们主要需要调参的是相似矩阵建立相关的参数和聚类类别数目，它对聚类的结果有很大的影响。当然其他的一些参数也需要理解，在必要时需要修改默认参数。

• n_clusters：代表我们在对谱聚类切图时降维到的维数，同时也是最后一步聚类算法聚类到的维数。也就是说scikit-learn中的谱聚类对这两个参数统一到了一起。简化了调参的参数个数。虽然这个值是可选的，但是一般还是推荐调参选择最优参数。
• affinity: 也就是我们的相似矩阵的建立方式。可以选择的方式有三类，第一类是 nearest_neighbors 即K邻近法。第二类是 precomputed 即自定义相似矩阵。选择自定义相似矩阵时，需要自己调用 set_params 来自己设置相似矩阵。第三类是全连接法，可以使用各种核函数来定义相似矩阵，还可以自定义核函数。最常用的是内置高斯核函数 rbf 。其他比较流行的核函数有 linear 即线性核函数, poly 即多项式核函数, sigmoid 即 sigmoid 核函数。如果选择了这些核函数， 对应的核函数参数在后面有单独的参数需要调。自定义核函数我没有使用过，这里就不多讲了。affinity默认是高斯核 rbf。一般来说，相似矩阵推荐使用默认的高斯核函数。
• 核函数参数gamma: 如果我们在 affinity 参数使用了多项式核函数 poly，高斯核函数 rbf, 或者 sigmoid 核函数，那么我们就需要对这个参数进行调参。
  • 多项式核函数中这个参数对应 \(K(x, z) = (\gamma x \cdot z+r)^d\) 中的 \(\gamma\) 。一般需要通过交叉验证选择一组合适的 \(\gamma, r, d\).
  • 高斯核函数中这个参数对应 \(K(x, z) = exp(-\gamma \Vert x - z\Vert^2)\) 中的 \(\gamma\) 。一般需要通过交叉验证选择合适的 \(\gamma\).
  • sigmoid核函数中这个参数对应 \(K(x, z) = tanh(\gamma x \cdot z+r)\) 中的 \(\gamma\) 。一般需要通过交叉验证选择一组合适的 \(\gamma, r\).
  • \(\gamma\) 默认值为1.0，如果我们affinity使用nearest_neighbors 或者是 precomputed，则这么参数无意义。
• 核函数参数degree：如果我们在affinity参数使用了多项式核函数 'poly'，那么我们就需要对这个参数进行调参。这个参数对应 \(K(x, z) = (\gamma x \cdot z+r)^d\) 中的 \(d\) 。默认是3。一般需要通过交叉验证选择一组合适的 \(\gamma, r, d\).
• 核函数参数coef0: 如果我们在 affinity 参数使用了多项式核函数 poly，或者 sigmoid 核函数，那么我们就需要对这个参数进行调参。
  • 多项式核函数中这个参数对应 \(K(x, z) = (\gamma x \cdot z+r)^d\) 中的 \(r\) 。一般需要通过交叉验证选择一组合适的 \(\gamma, r, d\).
  • sigmoid核函数中这个参数对应 \(K(x, z) = tanh(\gamma x \cdot z+r)\) 中的 \(r\) 。一般需要通过交叉验证选择一组合适的 \(\gamma, r\).
  • coef0 默认为 0
• kernel_params：如果affinity参数使用了自定义的核函数，则需要通过这个参数传入核函数的参数。
• n_neighbors: 如果我们affinity参数指定为 nearest_neighbors 即K邻近法，则我们可以通过这个参数指定KNN算法的K的个数。默认是10.我们需要根据样本的分布对这个参数进行调参。如果我们affinity不使用 nearest_neighbors，则无需理会这个参数。
• eigen_solver:在降维计算特征值特征向量的时候使用的工具。有 None,arpack, lobpcg, 和amg4种选择。如果我们的样本数不是特别大，无需理会这个参数，使用 None 暴力矩阵特征分解即可,如果样本量太大，则需要使用后面的一些矩阵工具来加速矩阵特征分解。它对算法的聚类效果无影响。
• eigen_tol：如果eigen_solver使用了 arpack，则需要通过eigen_tol指定矩阵分解停止条件。
• assign_labels：即最后的聚类方法的选择，有K-Means算法和 discretize算法两种算法可以选择。一般来说，默认的K-Means算法聚类效果更好。但是由于K-Means算法结果受初始值选择的影响，可能每次都不同，如果我们需要算法结果可以重现，则可以使用discretize。
• n_init：即使用K-Means时用不同的初始值组合跑K-Means聚类的次数，这个和K-Means类里面n_init的意义完全相同，默认是10，一般使用默认值就可以。如果你的n_clusters值较大，则可以适当增大这个值。

从上面的介绍可以看出，需要调参的部分除了最后的类别数n_clusters，主要是相似矩阵affinity的选择，以及对应的相似矩阵参数。当我选定一个相似矩阵构建方法后，调参的过程就是对应的参数交叉选择的过程。对于K邻近法，需要对n_neighbors进行调参，对于全连接法里面最常用的高斯核函数rbf，则需要对gamma进行调参。

参考资料：

• 用scikit-learn学习谱聚类.
• sklearn - API.

# 谱聚类
for i, g in enumerate((0.001, 0.01, 0.1, 1)):
    label = cluster.SpectralClustering(n_clusters=cnt_centers, gamma=g).fit_predict(dots)
    print(f"Calinski-Harabasz Score with gamma = {g} , score: {metrics.calinski_harabasz_score(dots, label)}")
    dots_cls = [color[lab] for lab in label]
    plt.figure(figsize=(4, 4), dpi=240)
    plt.scatter(dots[:,0], dots[:,1], c=dots_cls)
    plt.title(f"After - {g}")
    plt.savefig(f"2_{tag}_after_{i}.png", dpi=240)
    plt.show()

注：Calinski-Harbasz Score是通过评估类之间方差和类内方差来计算得分，越大代表着类自身越紧密，类与类之间越分散，即更优的聚类结果

点簇（密集）

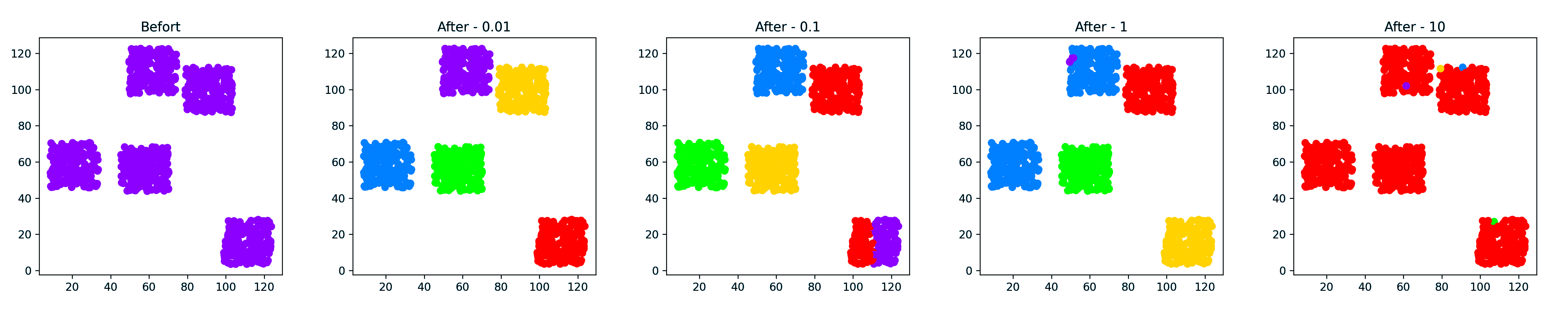
点簇（稀疏） - 10 类

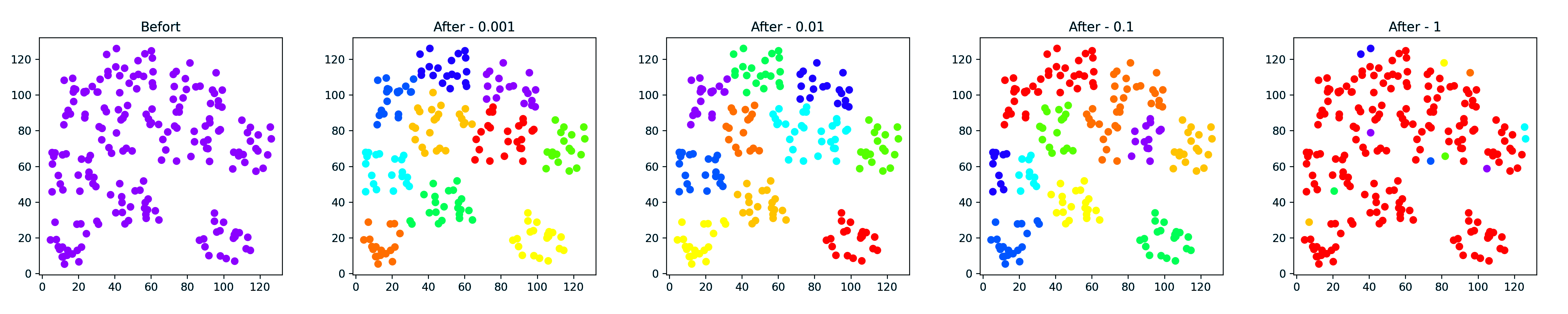
Calinski-Harabasz Score with gamma = 0.001 , score: 341.04076775146785
Calinski-Harabasz Score with gamma = 0.01 , score: 332.8219169560899
Calinski-Harabasz Score with gamma = 0.1 , score: 225.9696799273274
Calinski-Harabasz Score with gamma = 1 , score: 1.5146664858255785

随机

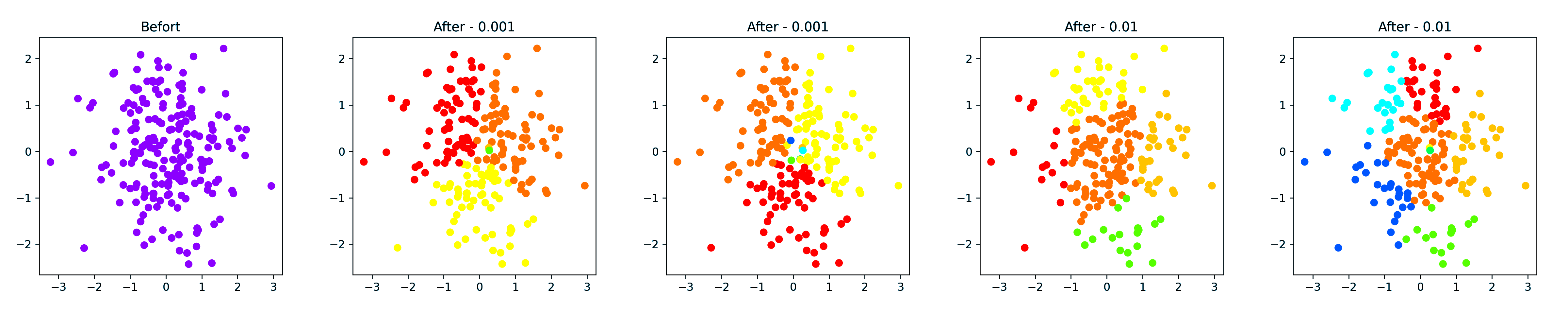
2,4 是分 5 类，3,5 是分 8 类

Calinski-Harabasz Score with gamma = 0.001 , score: 62.846443848710194
Calinski-Harabasz Score with gamma = 0.001 , score: 36.29822802071816
Calinski-Harabasz Score with gamma = 0.01 , score: 100.08933581499709
Calinski-Harabasz Score with gamma = 0.01 , score: 82.05754602148015

环形数据簇

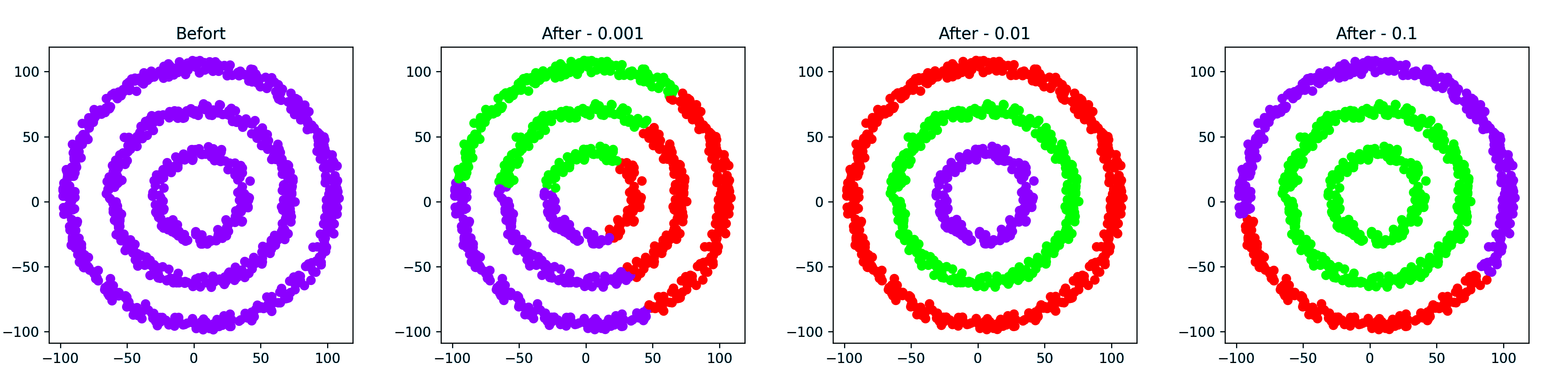
Calinski-Harabasz Score with gamma = 0.001 , score: 789.9927004062297
Calinski-Harabasz Score with gamma = 0.01 , score: 0.0017798081991424
Calinski-Harabasz Score with gamma = 0.1 , score: 181.06081887951328

这个时候 Calinski-Harabasz 评价不准，显然 0.01 的时候效果最好，下面螺旋同理，就不记录了

螺旋数据簇

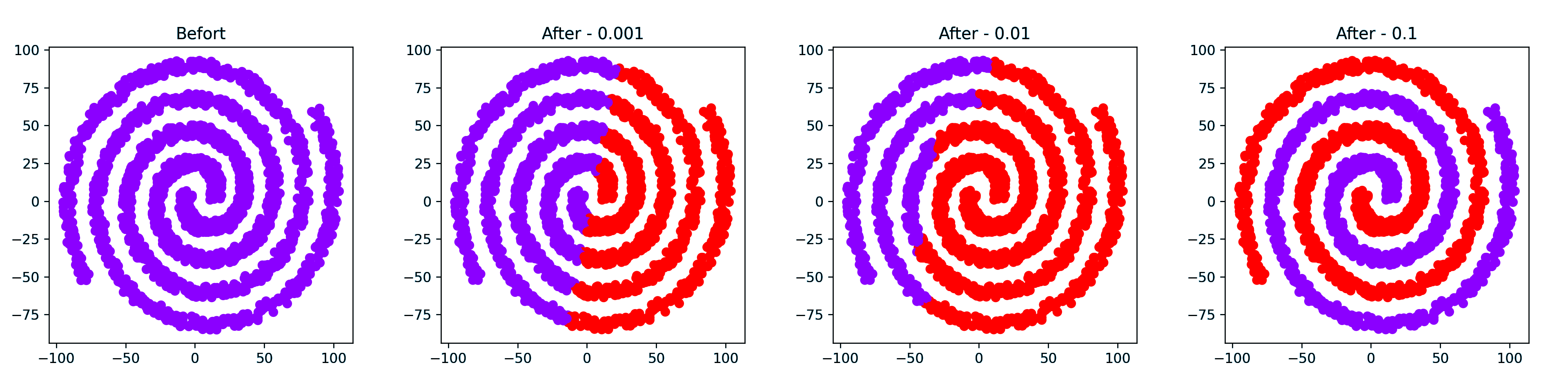
值得一提的是，前面的两个都是不到 1 秒就计算完成了，最后一个用了 1min 49s 才计算出来

测试得出的几个猜想：

• Calinski-Harabasz 分数不适合基于密度的聚类
• gmma 越小计算越快
• gamma 越大越倾向于基于密度聚类

---

近邻传播聚类

近邻传播聚类，即 AP（Affinity Propagation） 聚类

# Affinity Propagation 聚类
tag = "AffinityPropagation"
label = cluster.AffinityPropagation(damping=0.5).fit_predict(dots)
cnt_centers = max(label) + 2
print(cnt_centers - 2)
# 后面输出图像的代码和前面的几个一样，因为分开放在创建色卡步骤后面所以就忽略了

一个很大的缺点是复杂度很高，数据量大的时候相当慢，有分析指出每次迭代的复杂度是 \(O(n^3)\).

参考资料：

• sklearn - user guide
• sklearn api

点簇

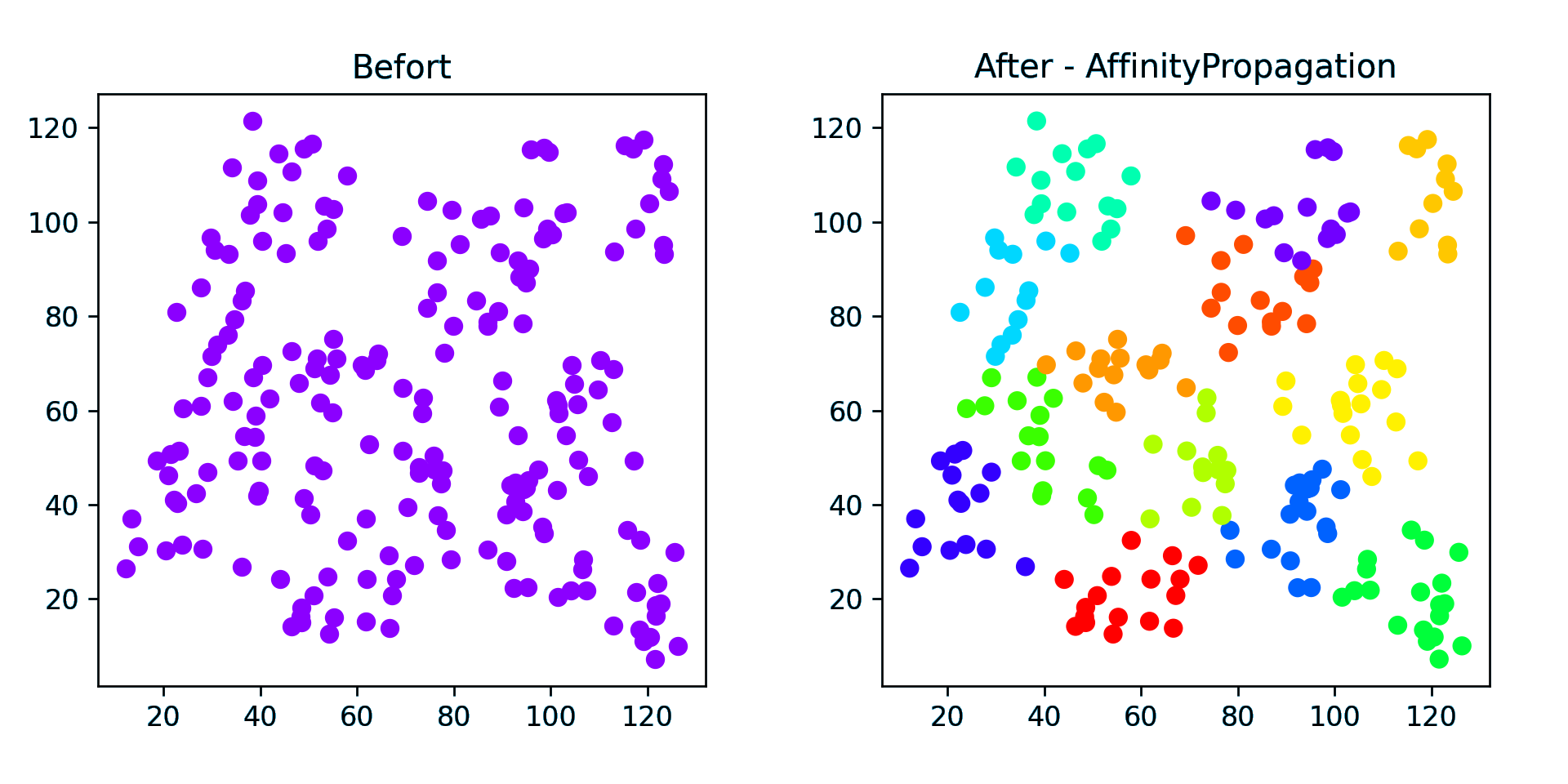
原 10 个中心点，聚类了 12 个类

随机（密集）

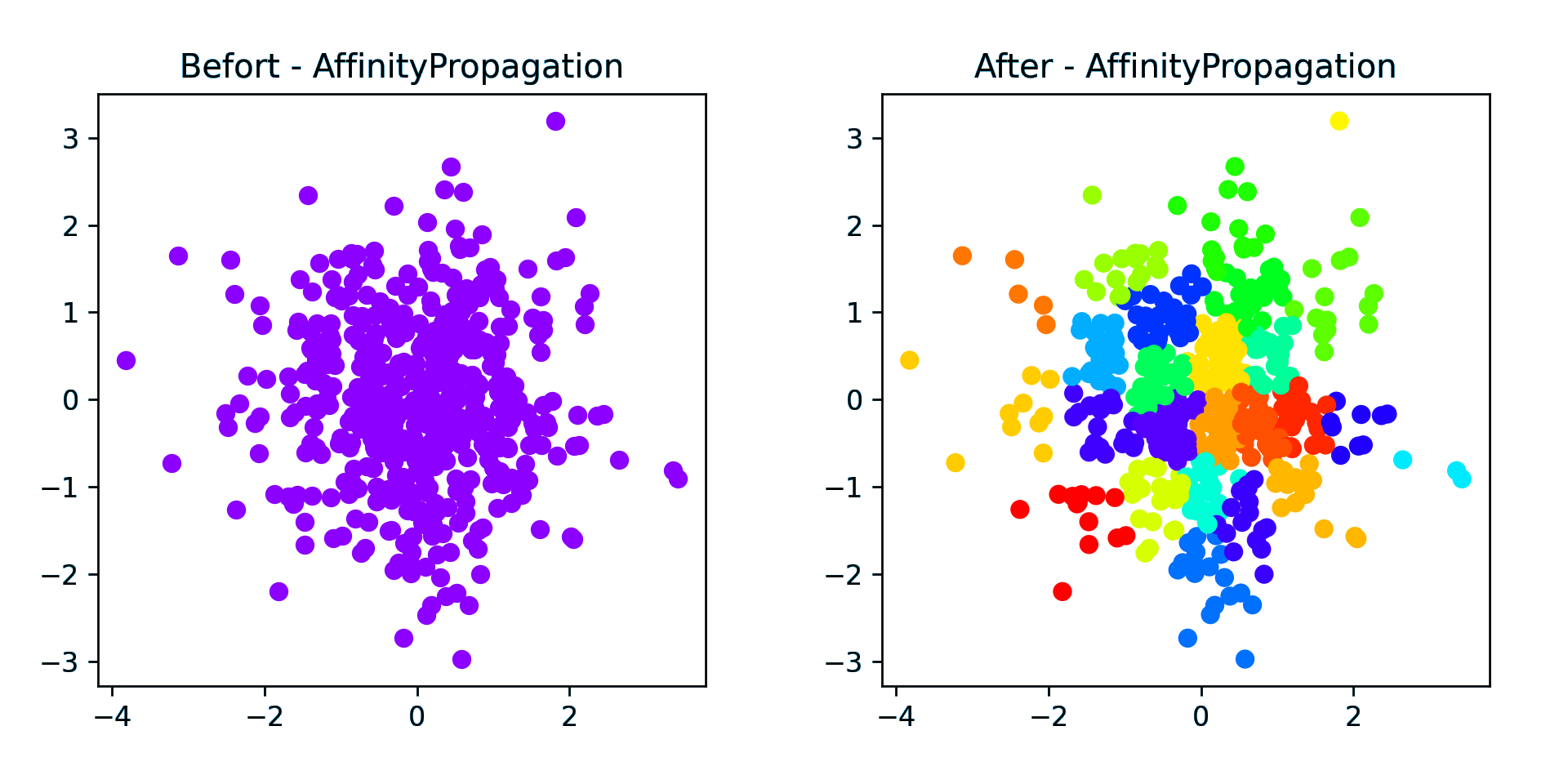
本来打算 2500 个点的，结果跑了十分钟没跑出来就放弃了，改成了 500 个点，1 秒钟就出结果了，24个聚类

环形点簇

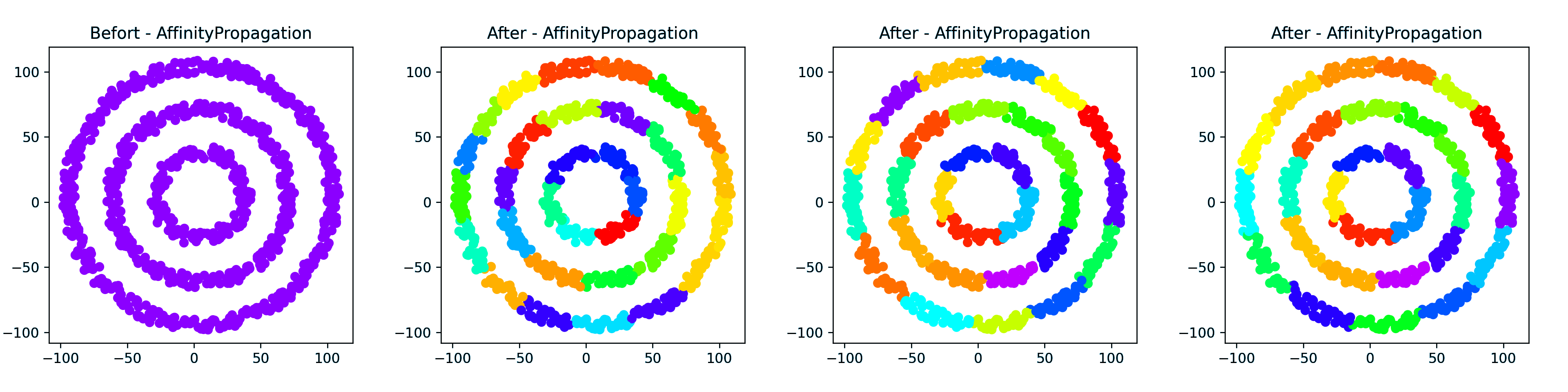
从左到右阻尼（damping）分别设置为 0.5（默认）,0.98,0.75，虽然不知道为什么，但第一个比后面两个慢好多好多

螺旋就不测了，点太多了估计要跑好久

---

层次聚类

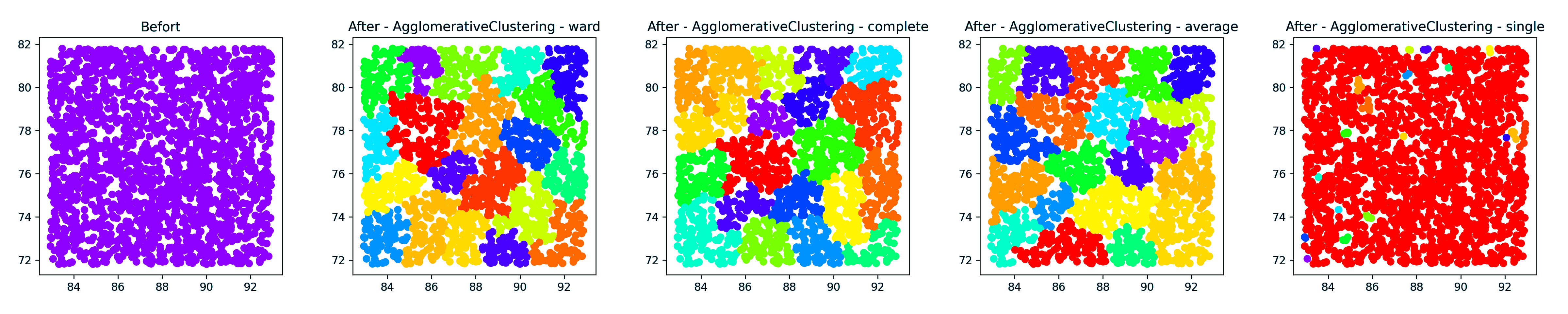
# 层次聚类 Agglomerative Clustering.
tag = "AgglomerativeClustering"
label = cluster.AgglomerativeClustering(n_clusters=cnt_centers, linkage='single').fit_predict(dots)
dots_cls = [color[lab] for lab in label]
plt.figure(figsize=(4, 4), dpi=240)
plt.scatter(dots[:,0], dots[:,1], c=dots_cls)
plt.title(f"After - {tag} - single")
plt.savefig(f"2_{tag}_after_3.png", dpi=240)
plt.show()

环形簇

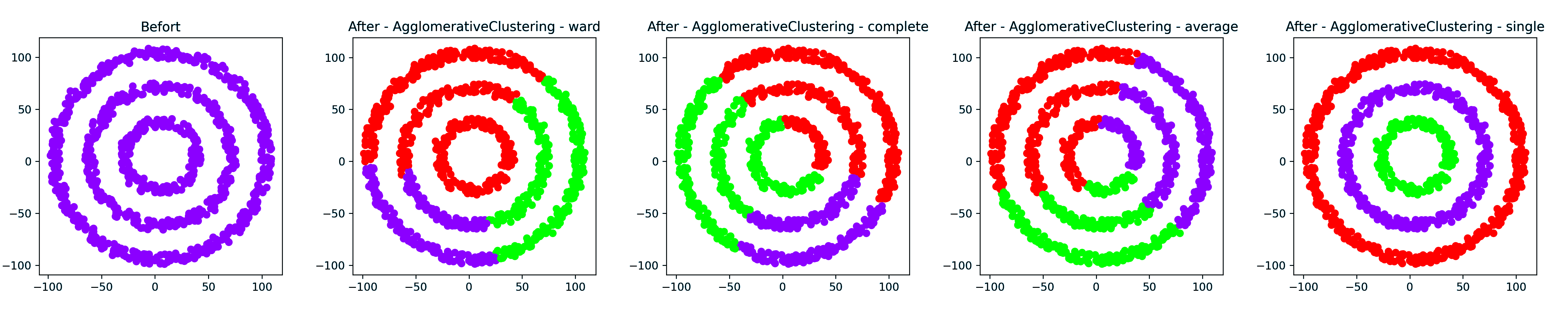
螺旋簇

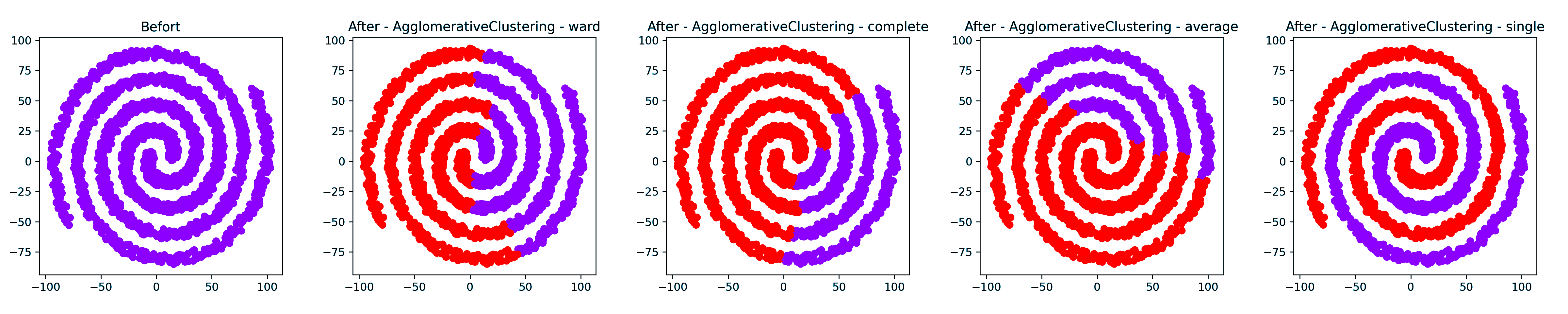
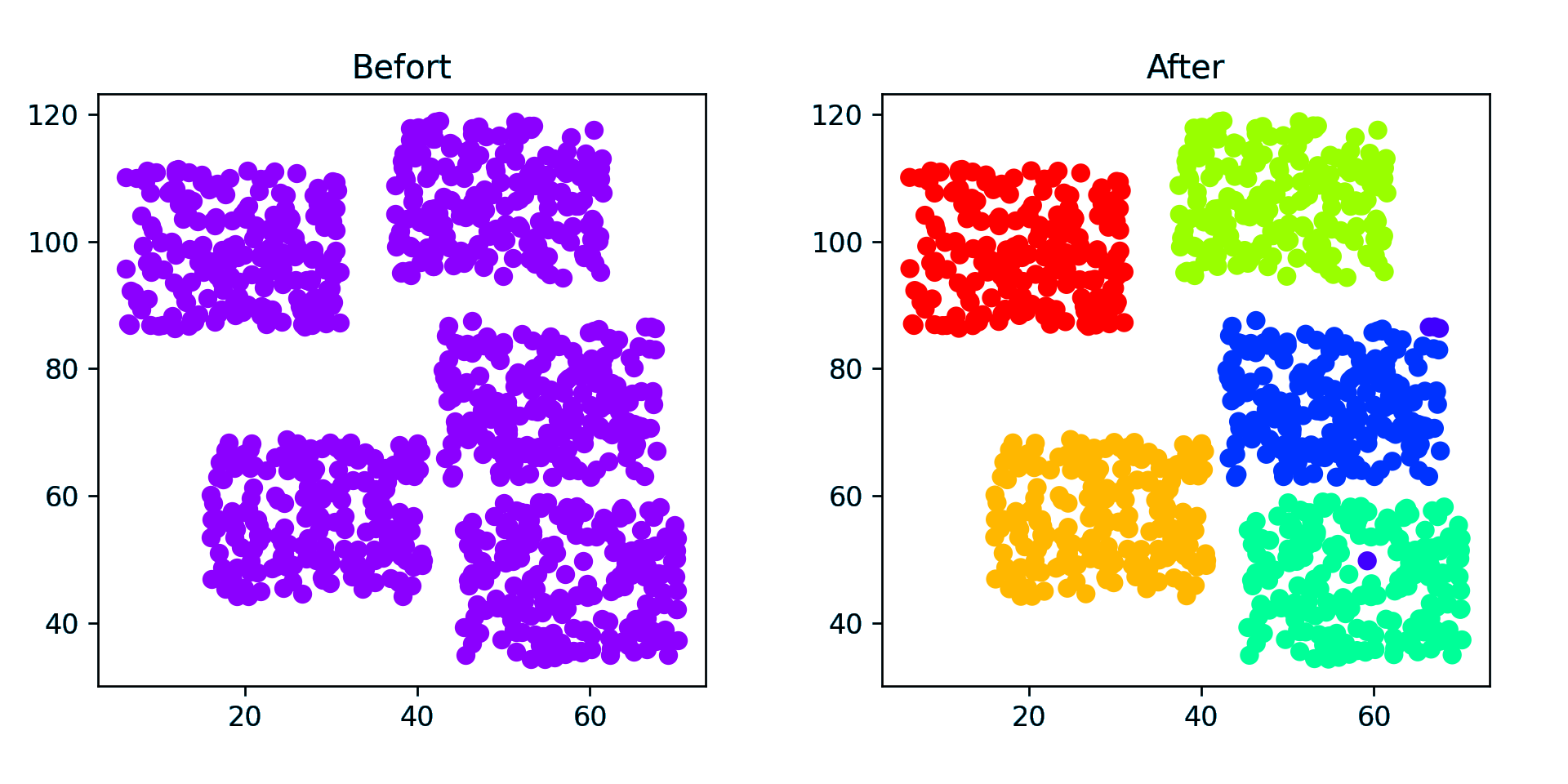
点簇（密集） - 20类