小鲸鱼的梦境
0%

『Python基础』heapq详解

发表于 更新于 分类于 Valine：
本文字数： 7.2k 阅读时长 ≈ 7 分钟

优先队列 - Priority queue

优先队列是一种特殊的队列，用于找出、返回并删除优先队列中最小(大)的元素。

优先队列的最简单实现就是二叉堆(binary heap), 简称堆(heap), 虽然优先队列还有其他一些更多功能、更复杂的实现，例如d-堆、左式堆(leftist heap)、斜堆(skew heap)、二项队列(binomial queue)等，但实践中最常用的还是堆，因此通常所说的堆和优先队列几乎是等同的，所以优先队列也可以称为最小(大)堆、小(大)根堆。

优先队列基本模型如下:

1
2
3
4
5
graph RL
    A[num] --Insert--> B((Priority Queue H))
    B[Priority Queue H] --DeleteMin--> C[ ]
    style A stroke-width:0px,fill-opacity:0
    style C stroke-width:0px,fill-opacity:0

堆 - heap

堆的两个性质

  • 结构性: 堆是一颗完全二叉树，因此可以使用线性的数组来实现而无需指针
  • 堆序性: 对于最小堆，要求根节点的值小于等于(\(\leq\))其左右节点的值

\(\qquad\)需要注意的是，堆序性是一种要求不太高的性质，蕴含的序的信息也不多，对于最小堆，仅有的信息是由根节点往页节点是非递减的，而对于堆中最大值或某个特定值的信息是没有的，唯一能确定的是，最大值位于叶结点，但半数的结点是叶结点，，因此该信息是无效的。

堆的操作(小根堆)

Insert(插入)

将元素X插入到堆, 为维持堆的堆序性，需要对新插入元素进行上滤(percolate up).

  1. 在堆的末尾插入X
  2. 检查X与其parent结点的值, 若X小于其parent结点，则交换parent结点与X，否则结束插入
  3. 重复执行step 2直到X成为根节点或不满足交换条件

\(\qquad\)在实现时，我们并不直接插入待插入元素在末尾，而是先在堆中查找待插入元素的插入位置，而在移动过程中可以直接将parent结点的值下移而无需执行交换，在一定程度上减少了赋值操作的次数。
\(\qquad\)最坏的情况，新插入的元素是最小值，并经过上滤到推到根节点的位置，其时间复杂度为\(O(log\\;n)\)

C代码如下:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* Code language: C */
/* H->Element[0] is a sentinel(哨兵/标记) */
void Insert(ElementType X, PriorityQueue H)
{
    int i;

    if (IsFull(H))
    {
        Error("Priority queue is full");
        return;
    }

    for(i = ++H->Size; H->Elements[i / 2] > X; i /= 2)
        H->Elements[i] = H->Elements[i / 2];
    H->Elements[i] = X;
}
DeleteMin(删除最小值)

\(\qquad\)由于堆的堆序性，很容易能找到堆的最小值是位于堆的第一个位置，但在删除后堆产生了一个空位，通常的做法是，将最末尾的元素移到空位然后执行下滤(percolate down).

  1. 设临时变量保存第一个位置的值(即最小值)
  2. 将最后一个位置的值移动到第一个位置
  3. 检查结点的值与其左右子节点的值，若结点值大于左右子节点值，那么选择值小的子节点进行交换
  4. 重复step 3直到结点成为叶子节点或不满足交换条件

\(\qquad\)同样的，下滤过程中也可以使用与上滤类似的技巧减少赋值次数。

\(\qquad\)取最小值的操作是\(O(1)\)时间复杂度的，而下滤操作最坏情况会下滤到叶子节点(事实上由于填补删除结点的结点来自叶子节点，下滤到叶子节点的可能性是相当大的), 其时间复杂度为\(O(log\\;n)\)

C代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/* Code language: C */
ElementType DeleteMin(PriorityQueue H)
{
    int i, Child;
    ElementType MinElement, LastElement;

    if (IsEmpty(H))
    {
        Error("Priority queue is empty");
        return H->Elements[0];
    }
    MinElement = H->Elements[1];
    LastElement = H->Elements[H->Size--];

    for (i = 1; i * 2 <= H->Size; i = Child)
    {
        /* Find smaller child */
        Child = i * 2;
        if (Child != H->Size && H->Elements[Child + 1] < H->Elements[Child])
            Child++;

        /* Percolate one level */
        if (LastElement > H->Elements[Child])
            H->Elements[i] = H->Elements[Child];
        else
            break;
    }
    H->Elements[i] = LastElement;
    return MinElement;
}
Build(建堆)

\(\qquad\)这里所说的建堆是指将一个完全无序的数组改造成堆，这在堆排序中进行了实现，其基本思想是: 由后往前遍历，对数组的每一个元素都执行上滤操作，原理是：每次上滤操作，都能使得当前遍历元素满足堆序性，当遍历完成即使得整个数组实现了堆序性。

python中的优先队列 - heapq模块

\(\qquad\)在python中，heapq模块提供了优先队列算法的实现，且堆的实现是建立在list的基础之上的。

函数原型

函数列表如下:

函数原型 作用 返回值
\(heapq.heappush(heap, item)\) 将 \(item\) 加入 \(heap\) 中 \(void\)
\(heapq.heappop(heap)\) 弹出并返回 \(heap\) 的最小的元素。如果堆空抛出 \(IndexError\) \(heap[0]\)
\(heapq.heappushpop(heap, item)\) 将 \(item\) 加入堆中，然后弹出并返回 \(heap\) 的最小元素
等效于先调用 \(heappush()\) 再调用 \(heappop()\)
\(heap[0]\)
\(heapq.heapify(x)\) 将\(list\\;x\) 转换成堆 \(void\)
\(heapq.heapreplace(heap, item)\) 弹出并返回 \(heap\) 的最小的元素，同时将 \(item\) 加入堆中, 如果堆空抛出 \(IndexError\)
等效于先调用 \(heappop()\) 再调用 \(heappush()\)
 \(heap[0]\)
\(heapq.merge(*iterables,key=None,reverse=False)\) 将多个已排序的输入合并为一个已排序的输出
\(key\) 指定带有单个参数的 \(key function\)，用于从每个输入元素中提取比较键, reverse 为一个布尔值
 已排序值的 \(iterator\)可迭代对象
\(heapq.nlargest(n, iterable, key=None)\) 等价于\(sorted(iterable, key=key, reverse=True)[:n]\) 前 \(n\) 个最大元素组成的列表
\(heapq.nsmallest(n, iterable, key=None)\) 等价于 \(sorted(iterable, key=key)[:n]\) 前 \(n\) 个最小元素组成的列表

\(\qquad\)在 \(heapq\) 的文档中有提示：后两个函数在 \(n\) 较小的时候会性能比较好，对于更大的值使用\(sort\)会更好。

小根堆 -> 大根堆

\(\qquad heapq\)是不提供大根堆的，具体原因就不去深究了，那么如果要使用大根堆要怎么办呢？
\(\qquad\)一个可行的方案是，入堆时将数取相反数，出堆时再取相反数，效果便等同于大根堆了。

使用示例

示例1

从List建堆: heapq.heapify(List)
1
2
# Code language: Python
heap = [67, 71, 65, 18, 75, 34, 78, 59, 45, 2, 38, 92, 26, 89, 80]

(待建立)堆示意图:

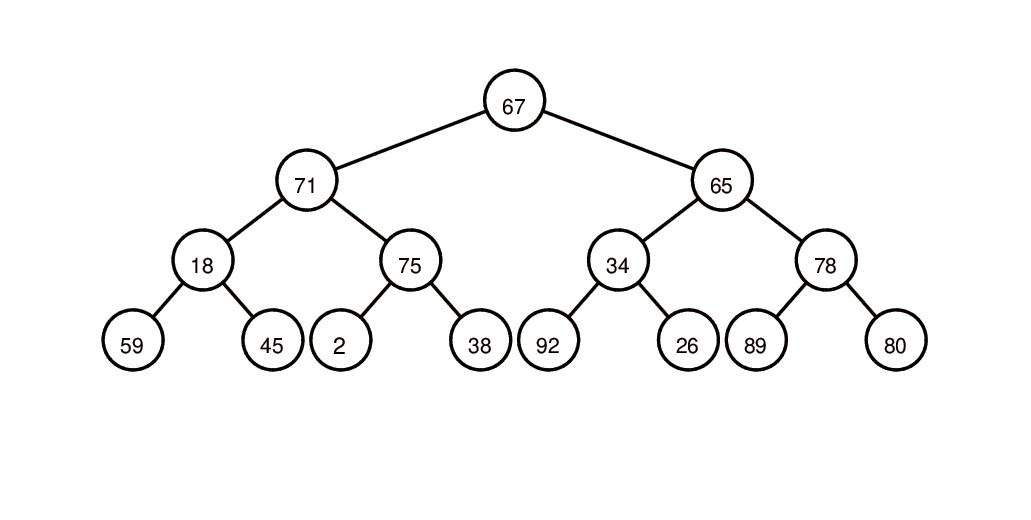
heap1

1
2
3
# Code language: Python
heapq.heapify(heap)
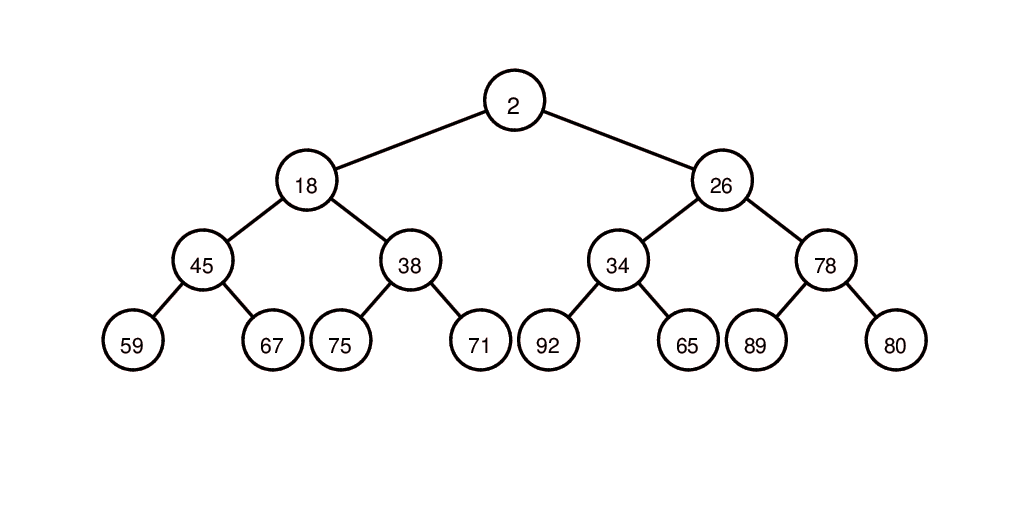
# heap: [2, 18, 26, 45, 38, 34, 78, 59, 67, 75, 71, 92, 65, 89, 80]

堆示意图:

heap2

取堆中最小元素: heapq.heappop(heap)

取堆中最小元素、将堆底元素补到堆顶，堆顶元素下滤

1
2
3
4
# Code language: Python
print(heapq.heappop(heap))
# output: 2
# heap: [18, 38, 26, 45, 71, 34, 78, 59, 67, 75, 80, 92, 65, 89]

堆示意图:

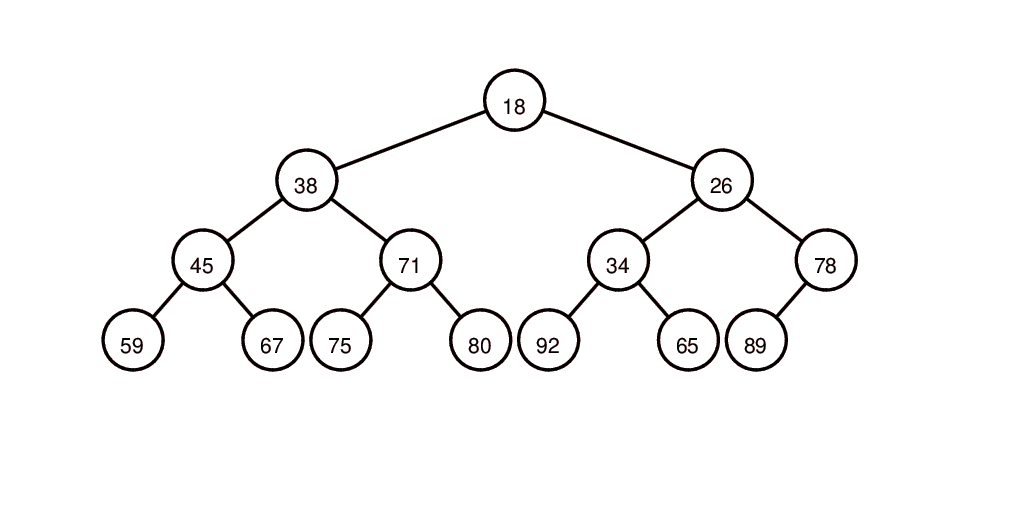
heap3

取堆中最小元素、将堆底元素补到堆顶，堆顶元素下滤

1
2
3
4
# Code language: Python
print(heapq.heappop(heap))
# output: 18
# heap: [26, 38, 34, 45, 71, 65, 78, 59, 67, 75, 80, 92, 89]

堆示意图:

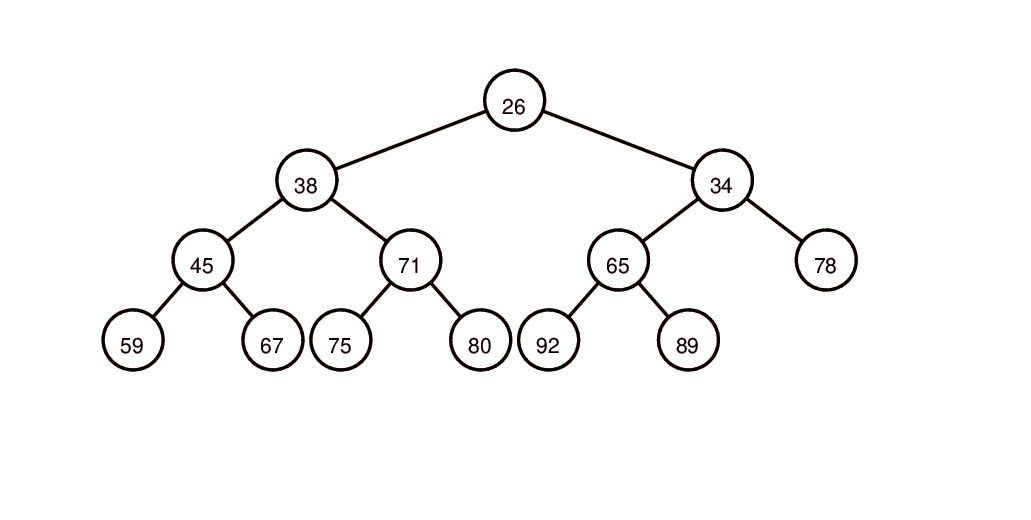
heap4

取堆中最小元素、将堆底元素补到堆顶，堆顶元素下滤

1
2
3
4
# Code language: Python
print(heapq.heappop(heap))
# output: 26
# heap: [34, 38, 65, 45, 71, 89, 78, 59, 67, 75, 80, 92]

堆示意图:

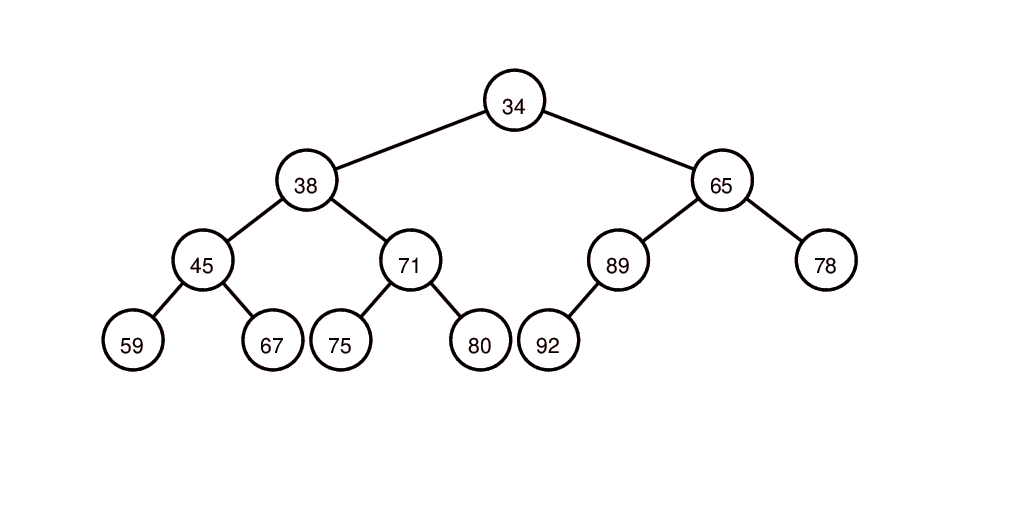
heap5

元素插入堆中: heapq.heappush(heap, item)

插入元素15:

1
2
3
# Code language: Python
heapq.heappush(heap, 15)
# heap: [15, 38, 34, 45, 71, 65, 78, 59, 67, 75, 80, 92, 89]

堆示意图:

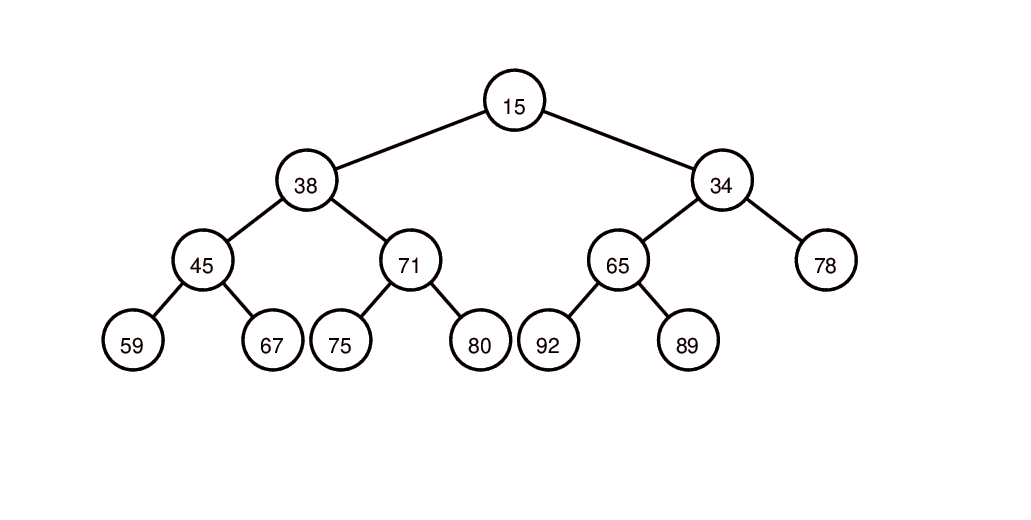
heap6

插入元素55:

1
2
3
# Code language: Python
heapq.heappush(heap, 55)
# heap: [15, 38, 34, 45, 71, 65, 55, 59, 67, 75, 80, 92, 89, 78]

堆示意图:

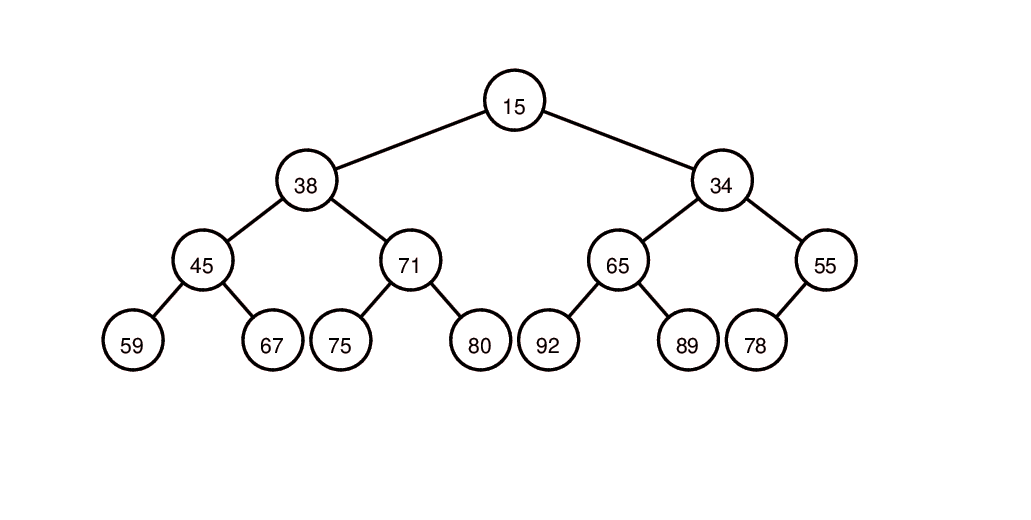
heap7

插入元素95:

1
2
3
# Code language: Python
heapq.heappush(heap, 95)
# heap: [15, 38, 34, 45, 71, 65, 55, 59, 67, 75, 80, 92, 89, 78, 95]

堆示意图:

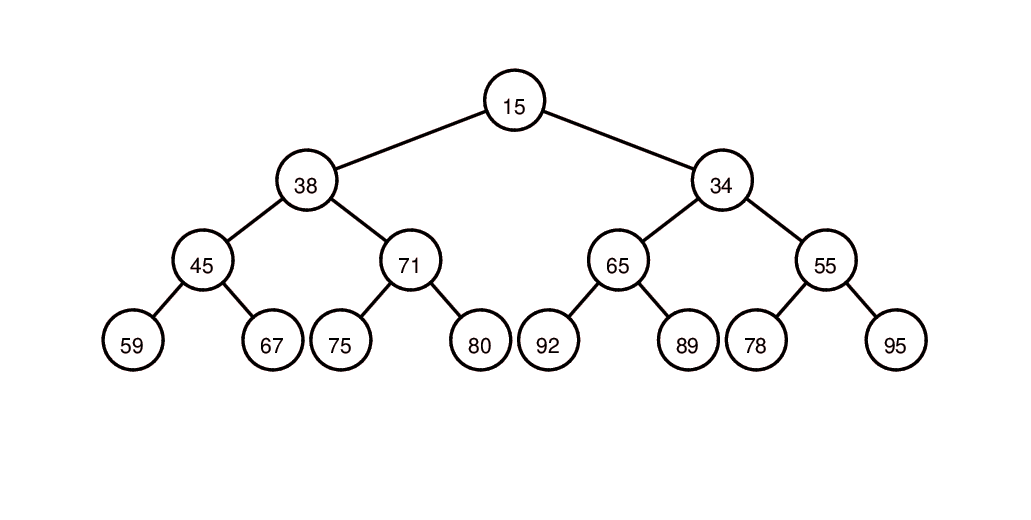
heap8

先插入元素到堆中再将最小元素取出: heapq.heappushpop(heap, item)

新加入元素可以先与堆顶元素做比较，若新元素不大于堆顶元素，什么堆中所有元素都不大于新加入元素，那么就无需执行插入操作直接返回新加入元素即可，若新元素大于于堆顶元素，那么问题就转换为了先取最小元素，再插入元素: heapq.heapreplace(heap, item)

插入元素1，取得元素1

1
2
3
4
# Code language: Python
print(heapq.heappushpop(heap, 1))
# output: 1
# heap: [15, 38, 34, 45, 71, 65, 55, 59, 67, 75, 80, 92, 89, 78, 95]

堆示意图:

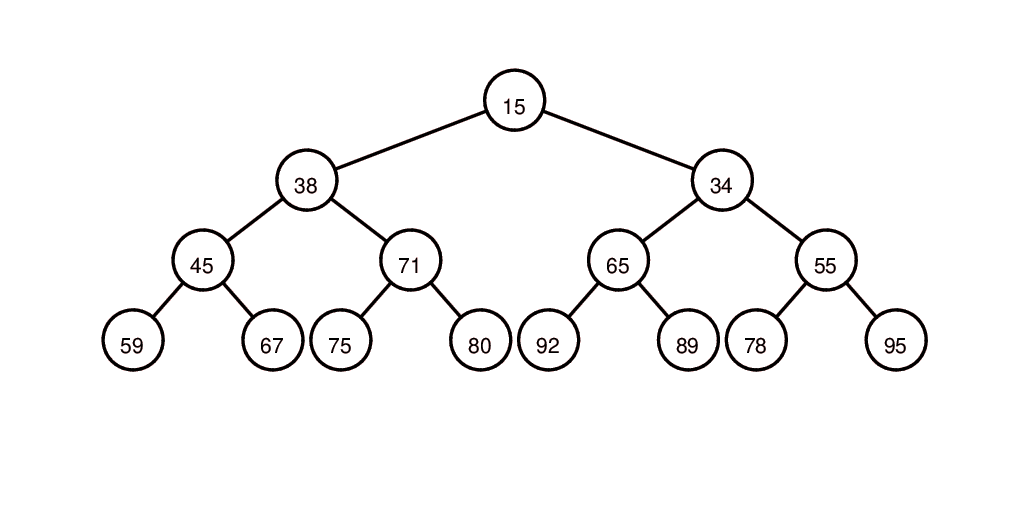
heap9

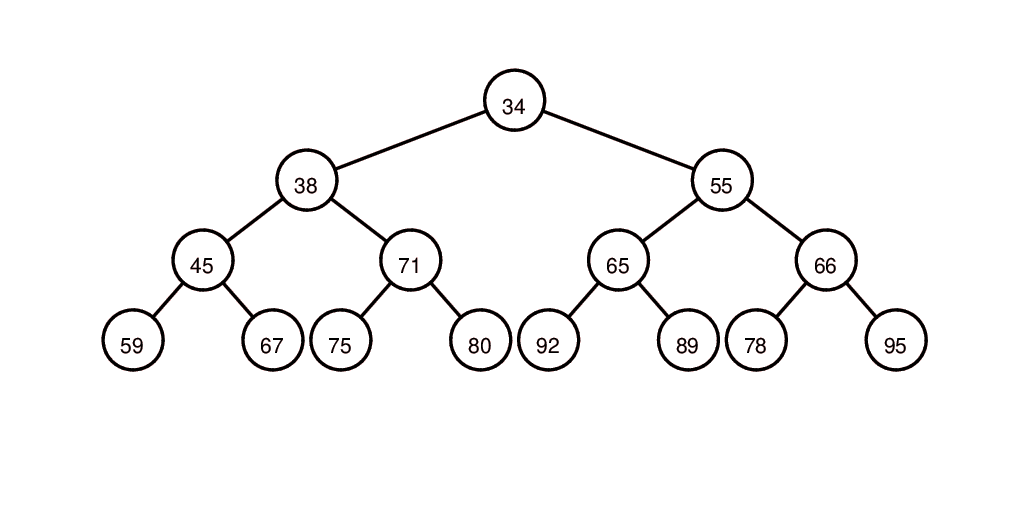
插入元素66，取得元素15

1
2
3
4
# Code language: Python
print(heapq.heappushpop(heap, 66))
# output: 15
# heap: [34, 38, 55, 45, 71, 65, 66, 59, 67, 75, 80, 92, 89, 78, 95]

堆示意图:

heap10

先取最小元素，再插入元素: heapq.heapreplace(heap, item)

新加入元素可以直接放在取走元素位置再执行下滤，减少了一轮下滤操作

插入元素1，取得元素34(区别heapq.heappushpop(heap, 1))

1
2
3
4
# Code language: Python
print(heapq.heapreplace(heap, 1))
# output: 34
# heap: [1, 38, 55, 45, 71, 65, 66, 59, 67, 75, 80, 92, 89, 78, 95]

堆示意图:

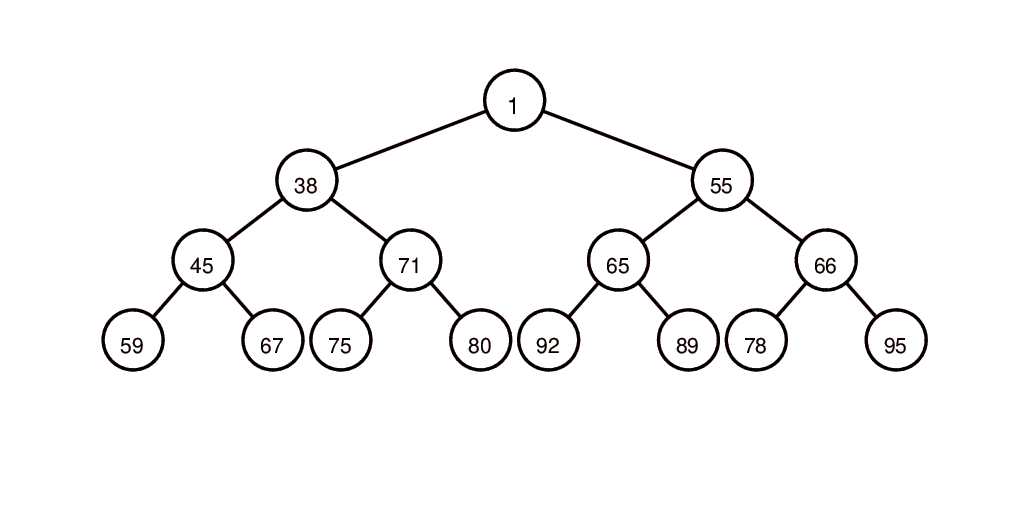
heap11

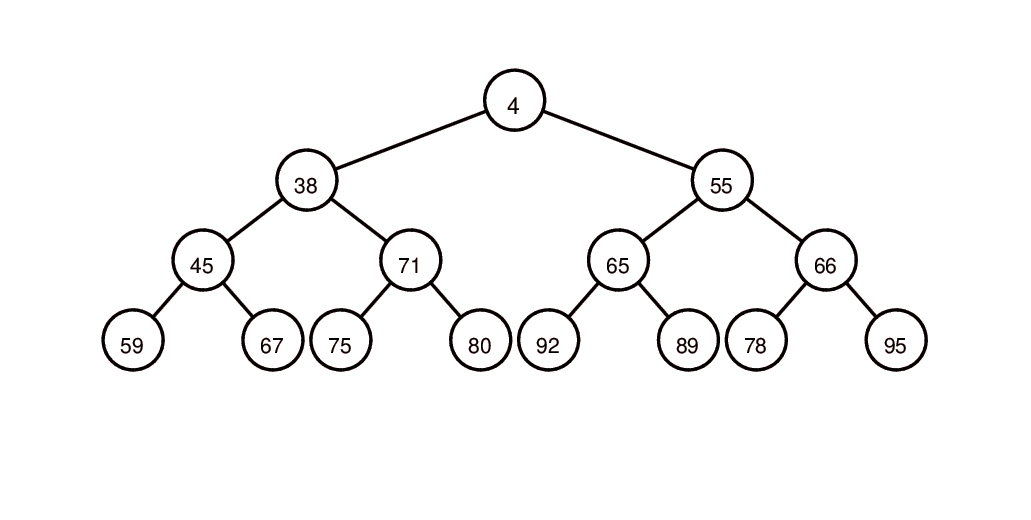
插入元素4，取得元素1

1
2
3
4
# Code language: Python
print(heapq.heapreplace(heap, 4))
# output: 1
# heap: [4, 38, 55, 45, 71, 65, 66, 59, 67, 75, 80, 92, 89, 78, 95]

堆示意图:

heap12

取n个最大的数: heapq.nlargest(n, iterable, key=None)
1
2
3
4
# Code language: Python
print(heapq.nlargest(5, heap))
# output: [95, 92, 89, 80, 78]
# heap: [4, 38, 55, 45, 71, 65, 66, 59, 67, 75, 80, 92, 89, 78, 95]

堆示意图:

heap13

取n个最小的数: heapq.nsmallest(n, iterable, key=None)
1
2
3
4
# Code language: Python
print(heapq.nsmallest(5, heap))
# output: [4, 38, 45, 55, 59]
# heap: [4, 38, 55, 45, 71, 65, 66, 59, 67, 75, 80, 92, 89, 78, 95]

堆示意图:

heap14

示例二

来看个算法问题吧：

魔塔游戏(来源LeetCode)

\(\qquad\)小扣当前位于魔塔游戏第一层，共有 \(N\) 个房间，编号为 \(0\\;-\\;N-1\)。每个房间的补血道具/怪物对于血量影响记于数组 \(nums\)，其中正数表示道具补血数值，即血量增加对应数值；负数表示怪物造成伤害值，即血量减少对应数值；\(0\) 表示房间对血量无影响。

\(\qquad\)小扣初始血量为 1，且无上限。假定小扣原计划按房间编号升序访问所有房间补血/打怪，为保证血量始终为正值，小扣需对房间访问顺序进行调整，每次仅能将一个怪物房间（负数的房间）调整至访问顺序末尾。请返回小扣最少需要调整几次，才能顺利访问所有房间。若调整顺序也无法访问完全部房间，请返回 -1。

示例1：

输入：nums = [100,100,100,-250,-60,-140,-50,-50,100,150] 输出：1 解释：初始血量为 1。至少需要将 nums[3] 调整至访问顺序末尾以满足要求。

示例2：

输入：nums = [-200,-300,400,0] 输出：-1 解释：调整访问顺序也无法完成全部房间的访问。

补充示例(非官方示例，仅说明特殊情况)：

输入：nums = [-2,1] 输出：1 解释：该示例运行LeetCode测试结果为1, 说明允许结束时血量为0，但不允许游戏过程中血量为0。

提示：

  • \(1\\;<=\\;nums.length\\;<=\\;10^5\)
  • \(-10^5\\;<=\\;nums[i]\\;<=\\;10^5\)
解题思路

\(\qquad\)不难想到，这题是使用贪心算法。在游戏中，无论是否调整，走到最后的血量都是固定的，也就是说调整并不会影响结果。
\(\qquad\)在访问过程中，每次调整都可以理解为回复一定的血量，将扣血的时间调整到最后。想要使得调整的次数最小，那么就要将已经访问过的怪物房间中扣血最多的那个调整到最后，所以在这个地方就要用到优先队列了。

解题步骤如下：

  • 顺序访问房间
  • 若遇到恢复房间，则正常通过，血量增加
  • 若遇到怪物房间，考察当前血量是否能通过
    • 血量足够，则正常通过，血量减少，怪物房间入队(heapq.heappush)
    • 血量不足, 则将怪物房间先入队，再出队扣血最多的怪物房间(调整到最后)(heapq.heappushpop)，最后正常通过
  • 访问结束，还剩下调整过的房间，只需考察剩余血量能否通过这些房间即可
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
# Code language: Python
class Solution:
    def magicTower(self, nums: List[int]) -> int:
        # 当前血量、房间数、调整次数、调整过的房间伤害总和
        cur, n, ans, s = 1, len(nums), 0, 0

        # 设优先队列存放路过的怪物房间
        heap = list()

        # 开始闯关~
        for i in range(n):
            # 拿到补血道具啦~
            if nums[i] >= 0:
                cur += nums[i]
            # 哎呀，遇到怪物了
            else:
                # 打不过了啦，只能发动技能惹 >_<
                if cur <= -nums[i]:
                    # 将当前房间加入怪物房间队列再将最强的怪物出队调整到最后
                    tmp = heapq.heappushpop(heap, nums[i])
                    cur += nums[i] - tmp # 注意怪物伤害是负数
                    s += tmp
                    ans += 1
                    # 需要判断血量是否为负吗？不需要哦，因为可以将当前房间调整到最后
                # 可以通过哦，痛击怪物吧~
                else:
                    cur += nums[i]
                    heapq.heappush(heap, nums[i])
        
        # 只剩下调整到最后的怪物房间了，看看剩余血量能不能支撑通过呢？
        if cur + s < 0:
            return - 1
            
        # 胜利啦
        return ans

运行结果：

魔塔游戏运行结果

--- ♥ end ♥ ---

欢迎关注我呀~