小鲸鱼的梦境
0%

『Python』Turtle绘制二叉树

发表于 更新于 分类于 Valine：
本文字数： 13k 阅读时长 ≈ 12 分钟

前言

\(\qquad\)二叉树是一种常见且用途极广的数据结构，但在使用过程中，二叉树的建立及具体结构却不太好考察，于是乎我试着使用 \(python\) 中一个基础的绘画库 —— \(Turtle\) 来将二叉树绘画到画板上。

绘制二叉树的实现

Step 1 导入库

1
2
3
4
import time, math, sys, os
import turtle
from typing import List
from PIL import Image

其中,

  • turtle —— python自带的基础绘图库，用于绘制二叉树
  • math —— 使用三角、反三角函数计算角度值
  • (可选)PIL.Image —— 用于将转换保存的 \(eps\) 文件为 \(png\) 文件
  • 其余的都是辅助，视个人需要导入

Step 2 二叉树结点的定义

1
2
3
4
5
6
# Code language: Python
class TreeNode(object):
    def __init__(self, val = 0, left = None, right = None):
        self.val = val
        self.left = left
        self.right = right

\(\qquad\)二叉树结点定义为具有结点值(\(value\))、指向左孩子的指针(\(left\))、指向右孩子的指针(\(right\))成员的类，其中结点初始值默认设为0，左右孩子指针均为空。

Step 3 二叉树的建立

\(\qquad\)二叉树结点定义好以后，就可以开始建立一棵二叉树啦~
\(\qquad\)这里我并不直接使用二叉树结点建立二叉树，而是采用一种类似层序遍历的方式来建立一棵二叉树。

  • 首先，建立 \(Tree\) 类，用于保存建立的二叉树，其初始化参数为一个结点值的列表，关于这个列表稍后会结合二叉树的建立说明列表值与二叉树结点的对应关系。
  • 对于一个 \(Tree\) 类，其成员属性有三个，分别是: 根节点(\(root\))、高度(\(height\))、遍历指针(\(PrintPoint\)), 其中遍历指针并不是必须的, 这里设置遍历指针是因为后面我采用了\(Morris\)遍历的迭代器，所以需要保存一个遍历指针。
  • 最后，如果传入的列表非空，则使用传入的列表初始化二叉树。
根据列表初始化二叉树

\(\qquad\)在常规的遍历方式中，一般需要两种方式的遍历结果才能唯一的确定一棵二叉树(前提是树中结点值不重复)，例如前序遍历+中序遍历、中序遍历+后序遍历、前序遍历+层序遍历等等、注意前序+后序的组合也无法完全确定二叉树，其根本原因是没法确定子树的根节点。
\(\qquad\)那么如何能根据遍历的列表就确定二叉树呢？一个可行的办法是列表中的二叉树是按完全二叉树的规则存储的，但这种办法的缺点是很可能会有大量的空间没有储存结点造成空间的浪费和输入的困难。

\(\qquad\)先看看层序遍历，接下来就能了解如何使用层序遍历的方法简化完全二叉树列表。

  1. 建立队列\(Queue\), 并将根节点入队;
  2. 队头结点出队，执行输出操作;
  3. 检查出队结点是否有孩子结点，若有，则依次将左、右孩子结点入队;
  4. 重复执行步骤2~3直到队列为空。

\(\qquad\)接下来再看看根据列表建立二叉树的步骤：

  1. 取列表首个元素作为二叉树的根节点的值(这里说的"取"均指删除并返回，若不希望改动列表也可以设置遍历指针并用指针后移操作代替删除);
  2. 建立队列\(Queue\), 并将根节点入队;
  3. 队头结点出队，取列表中前两个元素作为该节点的左右孩子的值;
  4. 若取出值为\(None\)，说明该节点没有左/右孩子结点;
  5. 将新建的孩子结点入队，重复执行2~5直到列表值取完(或遍历指针移动到列表末)。

\(\qquad\)可以看出，建立二叉树的方法与层序遍历是非常相似的，理解了层序遍历的操作以后很容易就能理解这种依据列表建立二叉树的方法。我们改变了完全二叉树存储方式中下标对应位置的规则，设置队列以层序遍历的方式来确定结点所在位置，从而避免了存储大量空结点，但需注意的是，列表的存储规则是按照层序遍历的结果存储，但对于度为1(即只有一个孩子的结点)的结点，必须添加\(None\)占位符在另一个孩子的位置，对于度为2, 0的结点则按照层序遍历结果确定位置。
\(\qquad\)换而言之，就是对于一个二叉树中的那些只有一个孩子的结点，需要补上一个"值为\(None\)"的结点使得树中所有结点都是度为2的结点或叶结点，再使用层序遍历得到列表，以此列表即可建立一棵唯一的二叉树。

\(\qquad\)这种方法虽然列表中也存在一些空的"\(None\)"结点，但度为1的结点在二叉树中最多不超过一半，所以这些冗余是可以接受的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Code language: Python
class Tree(object):
    def __init__(self, nums=None):
        self.root = None
        self.height = 0
        if nums:
            self.SetTree(nums)
        self.PrintPoint = self.root
    
    def SetTree(self, nums: List[int]):
        # 使用层序遍历的部分插入结点
        if not nums:
            return
        Queue = list()
        self.root = TreeNode(nums.pop(0))
        Queue.append(self.root)
        while nums:
            n = Queue.pop(0)
            nd = nums.pop(0)
            if nd:
                n.left = TreeNode(nd)
                Queue.append(n.left)
            if nums:
                nd = nums.pop(0)
                if nd:
                    n.right = TreeNode(nd)
                    Queue.append(n.right)
        # 计算二叉树高度并记录
        self.height = self.FindHeight(self.root)
    
    def FindHeight(self, root: TreeNode):
        # 递归计算二叉树高度
        if root:
            return max(self.FindHeight(root.left), self.FindHeight(root.right)) + 1
        else:
            return 0

\(\qquad\)最后，使用递归方法计算树的高度，这个是二叉树基本操作，就不赘述了~
\(\qquad\)也可以在建树的过程中设置标记域标记层数，在绘图过程中就使用了这种方法~

Step 4 二叉树的绘制

\(Turtle\)库的详细说明可以参考官方文档。

绘制过程主要有以下几个关键点:

  • 绘制树结点
    • \(Turtle\)有绘制圆的方法\(turtle.circle(radius,extent,steps)\)
      • radius -> 半径
      • extend -> 角度(默认整个圆即360)
      • step -> 步长, 其实圆是由正多边形画出的，所谓步长即正多边形边数
    • 使用goto函数到对应点然后绘制即可
    • 圆的半径可以考虑随深度减小，但会使代码逻辑复杂，故没有使用
    • \(Turtle\)有输出文字的方法\(urtle.write()\)
      • 考虑到圆的大小固定，文字大小位置会随文字的内容多少浮动，详细见代码
  • 连接两个结点
    • 难点在于确定绘画直线的角度
    • 只需确定两个结点的坐标即可调用\(math\)中的反三角函数得到角度值
    • 需要注意的是\(arctan(x)\)的取值范围是\((-90,90)\), 对于\(\pm 90\)即x坐标相同的情况需要单独处理
    • 对于两结点坐标顺序确定反三角函数不在取值范围的可以通过交换两结点坐标解决
    • 最后需要注意的就是结点的圆内不需要绘制连线
  • 确定结点所在坐标
    • 首先，根结点肯定位于画布中间偏上的位置
      • 综合考虑画布大小确定一个合适的值
    • 其次，一个结点的两个孩子之间的距离是随着树越深逐渐减小的
      • 设置偏移值\(dx,dy\)代表孩子结点与父母结点的偏移值
      • 其中孩子结点的\(y\)坐标统一减少\(dy\), \(dy\)不随深度变化
      • 两个孩子结点的\(x\)轴坐标为父母结点的\(x\)轴坐标\(\pm dx\), \(dx\)的值随深度增加而减少
      • 我并没有考虑在较深的一些层中只有较少的结点的情况，在这方面尚不完善
    • 最后，根据结点坐标层序的绘制出二叉树
      • 设置队列\(Queue\)，根结点入队
      • 队头结点出队，绘制队头结点
      • 检查队头结点，若有左孩子，则计算左孩子坐标，将左孩子入队，并绘制与左孩子的连线，右孩子同理
      • 重复前两步直到队列空
  • 最后的最后，将绘制好的画布保存为图片
    • 调用\(Turtle\)库函数可以将画布保存为\(eps\)文件(矢量图,可以用PS、AI打开)
    • 调用\(PIL\)库函数将\(eps\)文件转为\(png\)文件(不建议这么做，因为需要安装一个Ghoshscript的东西，并且转出来图片线条的锯齿非常明显)
    • 可以使用其他软件转换，如PS、AI等
    • 我使用的是\(irfanView\), 效果较调用\(PIL\)库函数平滑得多
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
# Code language: Python
def DrawTree(self, save = False):

    # 函数: 在指定位置绘制结点(传入结点及圆心坐标、结点深度)
    def drawnode(node: TreeNode, x: int, y: int):
        # 抬笔、到圆心下方、调整方向、绘制圆、抬笔、打印结点值
        turtle.penup()
        turtle.goto(x, y - radius)
        turtle.seth(0)
        turtle.pendown()
        turtle.circle(radius, steps=1024)
        turtle.penup()
        # 打印结点值、字体大小和位置随结点值字符长度浮动，但不小于临界值
        s = str(node.val)
        turtle.goto(x, y - radius + min(radius // 3 + len(s), 25))
        turtle.write(s, align="center", font=("Arial", max(25 - len(s) * 2, 8), "normal"))

    # 函数: 绘制两个结点之间的连线(传入两结点的圆心坐标)
    def drawlinknode(x1: int, y1: int, x2: int, y2: int):
        # arctan的取值范围是(-90,90)所以需将起始结点在结束结点右边的情况进行两结点的交换
        if x1 > x2:
            x1, y1, x2, y2 = x2, y2, x1, y1
        # 计算需要绘制连线的长度
        dis = max(((y2 - y1) ** 2 + (x2 - x1) ** 2) ** 0.5 - 2 * radius, 0)
        turtle.penup()
        turtle.goto(x1, y1)
        # 单独处理两结点在垂直方向相同的情况(即arctan为无穷, 会产生除0错)
        if x1 == x2 and y1 < y2:
            turtle.setheading(90)
        elif x1 == x2 and y1 > y2:
            turtle.setheading(-90)
        else: # 其他情况调用math库函数计算绘制直线的方向
            turtle.setheading(math.degrees(math.atan((y2 - y1) / (x2 - x1))))
        # 先出了所在圆，到边界再开始绘制
        turtle.fd(radius)
        turtle.pendown()
        turtle.fd(dis)
        turtle.penup()

    # 设置二叉树结点大小、每层高度
    radius = 30
    levelheight = 80

    # 设置窗口大小、颜色、标题
    turtle.setup(0.8, 0.8)
    width = 2 ** self.height * levelheight * 0.65 + 200
    height = levelheight * self.height + 200
    # print(width, height)
    turtle.screensize(width, height)
    turtle.clear()
    turtle.title("Draw Tree")
    # turtle.st()
    turtle.ht()
    turtle.tracer(False)# 不显示绘画过程
    turtle.colormode(255)
    turtle.pencolor("black")
    turtle.pensize(3)
    turtle.speed(0)
    turtle.shape("classic")

    # parent 和 children 之间的偏移量
    dx, dy = (width - 200) / 4, levelheight

    # 按照层序遍历的方法绘制二叉树
    # 队列中元素为: (结点, 横、纵坐标, 是否是该层最后一个结点)
    Queue = list()
    x, y = 0, height // 2 - 200
    if self.root:
        Queue.append([self.root, x, y, True])
    while Queue:
        cur = Queue.pop(0)
        drawnode(cur[0], cur[1], cur[2])
        if cur[0].left:
            i, j = cur[1] - dx, cur[2] - dy
            Queue.append([cur[0].left, i, j, False])
            drawlinknode(cur[1], cur[2], i, j)
        if cur[0].right:
            i, j = cur[1] + dx, cur[2] - dy
            Queue.append([cur[0].right, i, j, False])
            drawlinknode(cur[1], cur[2], i, j)
        if Queue and cur[3]:
            Queue[-1][3] = True
            dx = max(dx / 2, radius * 2 + 10)

    if save:
        # 存为.eps矢量图
        turtle.getcanvas().postscript(file="Tree.eps", x= -width / 2, y= -height / 2, height=height, width=width)
        # 借助PIL转换为.png (效果不好, 边缘锯齿严重, 远不如我用irfanView转换的效果好)
        # with open("Tree.eps", "rb") as fp:
        #     im = Image.open(fp)
        #     im.save("Tree.png")
        # with open("Tree.png", "rb") as fp:
        #     im = Image.open(fp)
        #     width, height = im.size
        #     im = im.resize((width * 2, height * 2))
        #     im.save("Tree.png")
        # 删除.eps文件(不建议删除，建议保留文件再使用工具转换)
        # os.remove("Tree.eps")
    else:
        turtle.done()

输出示例

示例1:
输入: list(range(127))

输出:

示例1-完全二叉树

示例2:
输入: [1, 2, 3, 4, None, 5, 6, None, None, None, 8]

输出:

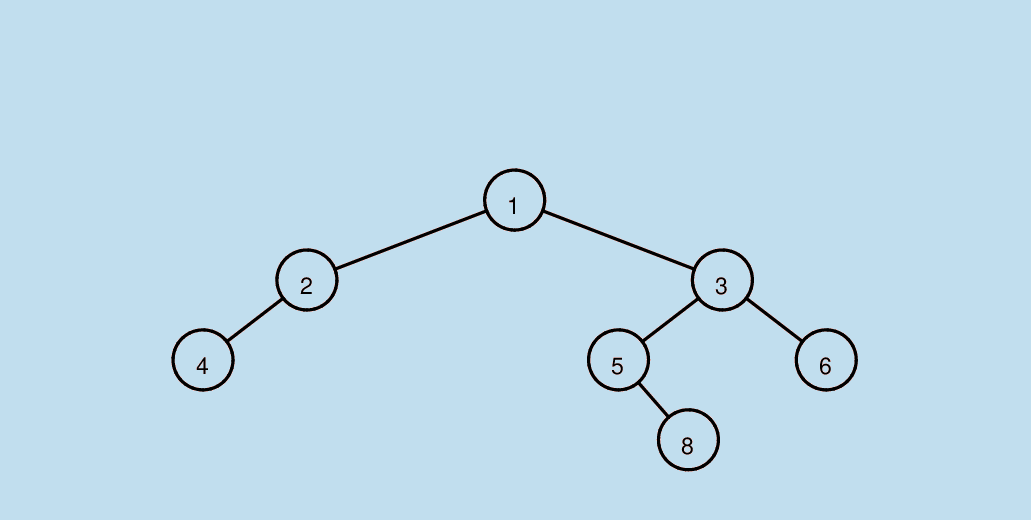
示例2-普通二叉树

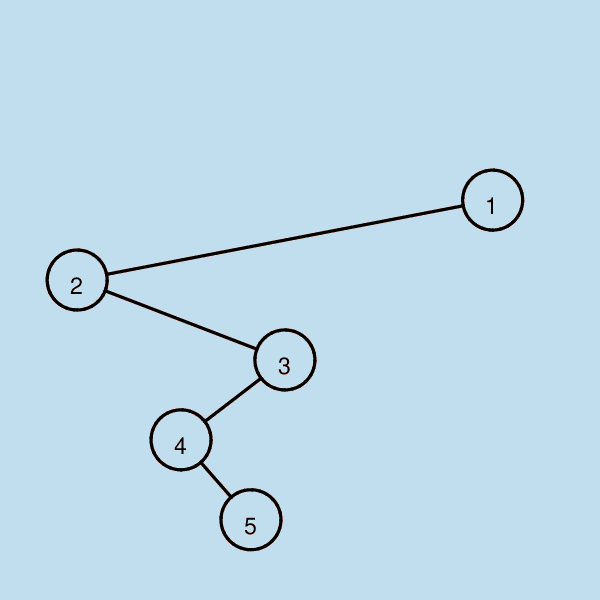
示例3:
输入: [1, 2, None, None, 3, 4, None, None, 5]

输出:

示例3-单枝二叉树

示例4:
输入: [1, 2, None, None, 3, 4, None, None, 5, None, 6, None, 7, 8]

输出:

示例4-深单枝二叉树

完整代码

\(\qquad Tree\)类中还添加了前序、中序、后序、层序遍历的实现，用于检测二叉树的情况，其中中序是使用\(Morris\)的方法实现的，前面也有提到过，具体二叉树的遍历方法可以看这篇文章

2021.04.16更新：
\(\qquad Tree\)类中添加参数filecount，用于计算输出的文件数量，解决了在多次执行DrawTree时保存的图片会覆盖的问题。
\(\qquad\)另外要注意的是传入类中的List会被修改，如果不希望传入List被修改，请使用Tree(List[:])的方法或提前复制。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
# -*- coding: utf-8 -*-
# Time    : 2021/04/12 19:16:16
# Author  : 小鲸鱼
# File    : Draw_Tree.py
# language: python
# Software: Visual Studio Code

import time, math, sys, os
import turtle
from typing import List
from PIL import Image

class TreeNode(object):
    def __init__(self, val = 0, left = None, right = None):
        self.val = val
        self.left = left
        self.right = right

class Tree(object):
    def __init__(self, nums=None):
        self.root = None
        self.height = 0
        self.filecount = 1
        if nums:
            self.SetTree(nums)
        self.PrintPoint = self.root
    
    def SetTree(self, nums: List[int]):
        # 使用层序遍历的部分插入结点
        if not nums:
            return
        Queue = list()
        self.root = TreeNode(nums.pop(0))
        Queue.append(self.root)
        while nums:
            n = Queue.pop(0)
            nd = nums.pop(0)
            if nd:
                n.left = TreeNode(nd)
                Queue.append(n.left)
            if nums:
                nd = nums.pop(0)
                if nd:
                    n.right = TreeNode(nd)
                    Queue.append(n.right)
        # 计算二叉树高度并记录
        self.height = self.FindHeight(self.root)
    
    def FindHeight(self, root: TreeNode):
        # 递归计算二叉树高度
        if root:
            return max(self.FindHeight(root.left), self.FindHeight(root.right)) + 1
        else:
            return 0
    
    def DrawTree(self, save = True):

        # 函数: 在指定位置绘制结点(传入结点及圆心坐标、结点深度)
        def drawnode(node: TreeNode, x: int, y: int):
            # 抬笔、到圆心下方、调整方向、绘制圆、抬笔、打印结点值
            turtle.penup()
            turtle.goto(x, y - radius)
            turtle.seth(0)
            turtle.pendown()
            turtle.circle(radius, steps=1024)
            turtle.penup()
            # 打印结点值、字体大小和位置随结点值字符长度浮动，但不小于临界值
            s = str(node.val)
            turtle.goto(x, y - radius + min(radius // 3 + len(s), 25))
            turtle.write(s, align="center", font=("Arial", max(25 - len(s) * 2, 8), "normal"))

        # 函数: 绘制两个结点之间的连线(传入两结点的圆心坐标)
        def drawlinknode(x1: int, y1: int, x2: int, y2: int):
            # arctan的取值范围是(-90,90)所以需将起始结点在结束结点右边的情况进行两结点的交换
            if x1 > x2:
                x1, y1, x2, y2 = x2, y2, x1, y1
            # 计算需要绘制连线的长度
            dis = max(((y2 - y1) ** 2 + (x2 - x1) ** 2) ** 0.5 - 2 * radius, 0)
            turtle.penup()
            turtle.goto(x1, y1)
            # 单独处理两结点在垂直方向相同的情况(即arctan为无穷, 会产生除0错)
            if x1 == x2 and y1 < y2:
                turtle.setheading(90)
            elif x1 == x2 and y1 > y2:
                turtle.setheading(-90)
            else: # 其他情况调用math库函数计算绘制直线的方向
                turtle.setheading(math.degrees(math.atan((y2 - y1) / (x2 - x1))))
            # 先出了所在圆，到边界再开始绘制
            turtle.fd(radius)
            turtle.pendown()
            turtle.fd(dis)
            turtle.penup()

        # 设置二叉树结点大小、每层高度
        radius = 30
        levelheight = 80

        # 设置窗口大小、颜色、标题
        turtle.setup(0.8, 0.8)
        width = 2 ** self.height * levelheight * 0.65 + 200
        height = levelheight * self.height + 200
        # print(width, height)
        turtle.screensize(width, height)
        turtle.clear()
        turtle.title("Draw Tree")
        # turtle.st()
        turtle.ht()
        turtle.tracer(False)
        turtle.colormode(255)
        turtle.pencolor("black")
        turtle.pensize(3)
        turtle.speed(0)
        turtle.shape("classic")

        # parent 和 children 之间的偏移量
        dx, dy = (width - 200) / 4, levelheight

        # 按照层序遍历的方法绘制二叉树
        # 队列中元素为: (结点, 横、纵坐标, 是否是该层最后一个结点)
        Queue = list()
        x, y = 0, height // 2 - 100
        if self.root:
            Queue.append([self.root, x, y, True])
        while Queue:
            cur = Queue.pop(0)
            drawnode(cur[0], cur[1], cur[2])
            if cur[0].left:
                i, j = cur[1] - dx, cur[2] - dy
                Queue.append([cur[0].left, i, j, False])
                drawlinknode(cur[1], cur[2], i, j)
            if cur[0].right:
                i, j = cur[1] + dx, cur[2] - dy
                Queue.append([cur[0].right, i, j, False])
                drawlinknode(cur[1], cur[2], i, j)
            if Queue and cur[3]:
                Queue[-1][3] = True
                dx = max(dx / 2, radius * 2 + 10)

        if save:
            # 存为.eps矢量图
            turtle.getcanvas().postscript(file="Tree" + str(self.filecount) + ".eps", x= -width / 2, y= -height / 2, height=height, width=width)
            self.filecount += 1
            # 借助PIL转换为.png (效果不好边缘锯齿严重，远不如我用irfanView转换的效果好)
            # with open("Tree.eps", "rb") as fp:
            #     im = Image.open(fp)
            #     im.save("Tree.png")
            # with open("Tree.png", "rb") as fp:
            #     im = Image.open(fp)
            #     width, height = im.size
            #     im = im.resize((width * 2, height * 2))
            #     im.save("Tree.png")
            # 删除.eps文件(不建议删除，建议保留文件再使用工具转换)
            # os.remove("Tree.eps")
        else:
            turtle.done()

    def nextnode(self) -> int:
        # 扁平化二叉搜索树迭代器，中序输出树节点
        while self.PrintPoint:
            # 存在左子树，则左子树的最右节点存放指向该节点的线索(指针)
            if self.PrintPoint.left:
                mostright = self.PrintPoint.left
                # 查找左子树最右节点
                while mostright.right and not mostright.right == self.PrintPoint:
                    mostright = mostright.right
                # 若查找结果不为空(回到根节点)，说明左子树最右节点已经存放了线索并且左子树已经遍历过，抹去该线索
                if mostright.right:
                    mostright.right = None
                # 若结果为空，存入线索，根节点左移(root = root->left)，重复查找
                else:
                    mostright.right = self.PrintPoint
                    self.PrintPoint = self.PrintPoint.left
                    continue
            # 根节点不存在左子树或左子树已经遍历过，输出该节点，再将根节点右移(root = root->right)
            ans = self.PrintPoint.val
            self.PrintPoint = self.PrintPoint.right
            return ans

    def PrintMidTree(self):
        # 利用线索在O(1)空间中序遍历二叉树(不改动树本身)
        print("中序遍历: ", end="")
        self.PrintPoint = self.root
        while self.PrintPoint:
            print(self.nextnode(), end=" ")
        print()

    def PrintPreTree(self):
        # 递归前序遍历二叉树
        def PreVisit(root: TreeNode):
            if root:
                print(root.val, end= " ")
                PreVisit(root.left)
                PreVisit(root.right)

        print("前序遍历: ", end="")
        PreVisit(self.root)
        print()

    def PrintPostTree(self):
        # 递归后序遍历二叉树
        def PostVisit(root: TreeNode):
            if root:
                PostVisit(root.left)
                PostVisit(root.right)
                print(root.val, end= " ")

        print("后序遍历: ", end="")
        PostVisit(self.root)
        print()
    
    def PrintLevelTree(self):
        # 层序遍历二叉树
        Queue = list()
        print("层序遍历: ", end="")
        if self.root:
            Queue.append(self.root)
        while Queue:
            cur = Queue.pop(0)
            print(cur.val, end=" ")
            if cur.left:
                Queue.append(cur.left)
            if cur.right:
                Queue.append(cur.right)
        print()



if __name__ == "__main__":
    start = time.perf_counter()

    # 测试1: 完全二叉树
    # T = Tree(list(range(127)))
    # T.DrawTree(1)

    # 测试2
    # T = Tree([1, 2, 3, 4, None, 5, 6, None, None, None, 8])
    # T.PrintPreTree()
    # T.PrintMidTree()
    # T.PrintPostTree()
    # T.PrintLevelTree()
    # print("TreeHeight = ", T.height)
    # T.DrawTree(1)

    # 测试3
    # T = Tree([1, 2, None, None, 3, 4, None, None, 5])
    # T.PrintPreTree()
    # T.PrintMidTree()
    # T.PrintPostTree()
    # T.PrintLevelTree()
    # print("TreeHeight = ", T.height)
    # T.DrawTree(1)

    # 测试4
    T = Tree([1, 2, None, None, 3, 4, None, None, 5, None, 6, None, 7, 8])
    T.PrintPreTree()
    T.PrintMidTree()
    T.PrintPostTree()
    T.PrintLevelTree()
    print("TreeHeight = ", T.height)
    T.DrawTree(1)

    end = time.perf_counter()
    print("Running Time: {:,.2f}μs".format((end - start) * 10 ** 6))
--- ♥ end ♥ ---

欢迎关注我呀~