小鲸鱼的梦境
0%

『论文笔记』Global Filter Networks for Image Classification

发表于 更新于 分类于 Valine：
本文字数： 3.8k 阅读时长 ≈ 3 分钟

Information

  • Title: Global Filter Networks for Image Classification
  • Author: Yongming Rao, Wenliang Zhao
  • Institution: 清华大学
  • Year: 2021
  • Journal: NeurIPS
  • Source: NeurIPS, Arxiv, Project Page, Github, OpenReview
  • Cite: Rao Y, Zhao W, Zhu Z, et al. Global filter networks for image classification[J]. Advances in neural information processing systems, 2021, 34: 980-993.
  • Idea: 提出了一种全局滤波网络，由傅里叶变换和可学习的一组滤波器代替 self-attention，更高效
1
2
3
4
5
6
7
@article{rao2021global,
  title={Global Filter Networks for Image Classification},
  author={Rao, Yongming and Zhao, Wenliang and Zhu, Zheng and Lu, Jiwen and Zhou, Jie},
  journal={Advances in Neural Information Processing Systems},
  volume={34},
  year={2021}
}

Abstract

作者提出了全局滤波器网络(Global Filter Networks, GFNet)，可以替代 transformer 中的 self-attention 层且其计算时间复杂度更优。

Introduction

Transformer 和纯 MLP 网络的一个问题是其对于 token 数量的增加计算复杂度是二次方增加的，这带来了一些限制。

作者提出了一种新的结构 GFNet 只需要对数线性复杂度就能达到相近的效果，其中的基本观点是学习频域中空间位置之间的相互作用。作者将 token 之间的交互建模为一组可学习的全局滤波器用于输入特征的频谱，由于全局滤波器能覆盖所有频段，所以该模型能同时捕获长短期交互。

作者提出的框架基本基于视觉 transformer 仅仅用三个关键操作替换了 self-attention 层：二维离散傅里叶变换、频域特征和全局滤波器之间的逐元素乘法、二维逆傅里叶变换。FFT的时间复杂度是 𝒪(Llog L) 比 self-attention 和 MLP 更有效。因此其对于 token 长度 L 不敏感所以对大的 feature map 和类 CNN 结构的网络兼容性较好。

fig1

时间复杂度的比较如下表：

image-20230421164343276

Method

离散傅里叶变换

首先作者介绍了离散傅里叶变换(DFT)，对于 1D 离散傅里叶变换，给定长度为 N 的复数序列 x[n], 0 ≤ n ≤ N − 1, 1D 离散傅里叶变换可以表示为 $$ X[k]=\sum_{n=0}^{N-1} x[n] e^{-j(2\pi / N) k n} := \sum_{n=0}^{N-1} x[n] W_N^{kn} $$ 其中 j 是虚数单位且 WN = e−j(2π/N). 因为 X[k] 在长度 N 的间隔上重复，所以只需要在 N 个连续点 k = 0, 1, …, N − 1 采样 X[k] 的值即可。这里 X[k] 表示序列 x[n] 在频域 ωk = 2πk/N 的频谱。

因为 DFT 是一一对应的转换，所以给定 DFT X[k] 可以通过逆 DFT(IDFT) 恢复原始信号 x[n] : $$ x[n] = \frac{1}{N} \sum_{k=0}^{N - 1}X[k]e^{j(2\pi/N)kn}. $$ 对于实数输入 x[n], 可以证明其 DFT 是共轭对称的，即 X[N − k] = X*[k]. 同样的对共轭对称的 X[k] 进行逆傅里叶变换我们能得到实离散信号。这说明一半的DFT {X[k] : 0 ≤ k ≤ ⌈N/2⌉} 就包含了 x[n] 的全部频域特征信息。

DFT 广泛用于建模信号处理主要是因为有两个优点：

  1. 输入输出都是离散的过程，易于用计算机进行处理
  2. 存在有效的算法计算DFT：FFT 利用WNkn 对称和周期的性质将 DFT 的计算量由 𝒪(N2) 减少到了 𝒪(Nlog N)，类似的逆傅里叶变换同样有高效的逆快速傅里叶变换算法

将 DFT 用于二维的信号：给定二维信号 X[m, n], 0 ≤ m ≤ M − 1, 0 ≤ n ≤ N − 1 二维 DFT x[m, n] 如下： $$ X[u, v] = \sum_{m=0}^{M-1}\sum_{n=0}^{N-1}x[m, n]e^{-j2\pi\left(\frac{um}{M}+\frac{vn}{N}\right)}. $$

2D DFT 可以视为 1D DFT 在两个维度的应用，同理2D DFT 对实输入 x[m, n] 满足共轭对称的性质 X[M − u, N − v] = X*[u, v], 同样可以使用 FFT 加速运算。

GFNet

结构如图所示，一个基础的模块包含：

  1. 全局滤波层，可以高效交换空间信息
  2. 一个前向传播网络

对于全局滤波层，给定 token x ∈ ℝH × W × D,首先使用 2D DFT 在空间维度将 x 转换到频域： X = ℱ[x] ∈ ℂH × W × D, 其中 ℱ[⋅] 表示 2D DFT，得到的 X 是一个复数。随后将可学习的滤波器 K ∈ ℂH × W × D 与 X 相乘： X̃ = K ⊙ X, 其中 ⊙ 是逐元素乘法，滤波器 K 称为全局滤波器是因为它与 X 有相同的维度，可以代表频域中任意滤波器。最后应用逆傅里叶变换将 X̃ 变换会空域并更新 token x ← ℱ−1[X̃]. 作者提出的全局滤波层是受到数字图像处理中的频率滤波的启发，可以看作是一组针对不同隐藏维度的频率滤波器。可以证明全局滤波层等价与一个逐深度的全局循环卷积，其滤波核大小为 H × W. 虽然全局滤波器也可以解释为空域操作，但作者认为全局滤波器具有更清晰的模式，也倾向于捕捉频域的关系。同时，还有一个优势是全局滤波层比空域操作更高效。

因为输入的 x 都是实数，即 X[H − u, W − v,  : ] = X*[H, W,  : ] 共轭对称，所以只用一半的信息即可： Xr = X[:,0 : Ŵ] := ℱr[x],  Ŵ = ⌈W/2⌉, 其中 ℱr 表示用于实输入的 2D DFT. 在这种方式下全局过滤核为 Kr ∈ ℂH × Ŵ × D, 同样可以减少一半的参数，同样可以保证 ℱr−1[Kr ⊙ Xr] 也是实数，可以与 x 直接做残差连接。并且实现也很简单：

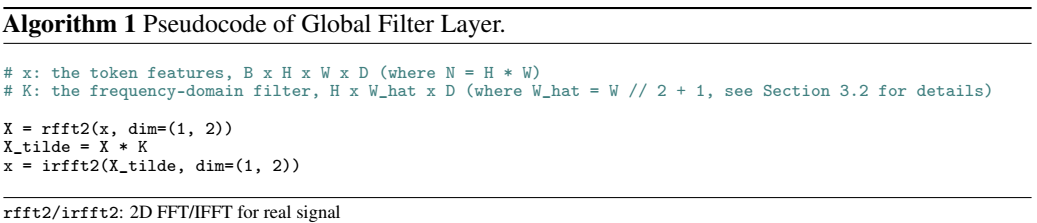
image-20230422145843401

对比已有的 Transformer 和 MLP 网络，GFNet 有以下优势：

  1. 高效，计算复杂度为 𝒪(Llog L) 比 Transformer 和 MLP 的 𝒪(L2) 更高效
  2. 可拓展性。傅里叶变换是无需参数的，而全局滤波器 K′ ∈ ℂH′ × W′ × D 可以很容易的通过插值的方式对于任意尺寸的输入拓展，这是由 DFT 的性质保证的：全局滤波器 K[u, v] 的每一个元素对应滤波器在 ωu = 2πu/H, ωv = 2πv/W 的频谱，全局滤波器 K 可以看作一个连续的频谱 K(ωu, ωv) 其中 ωu, ωv ∈ [0, 2π]，因此改变输入图像的分辨率等价于改变 K(ωu, ωv) 的采样间隔。

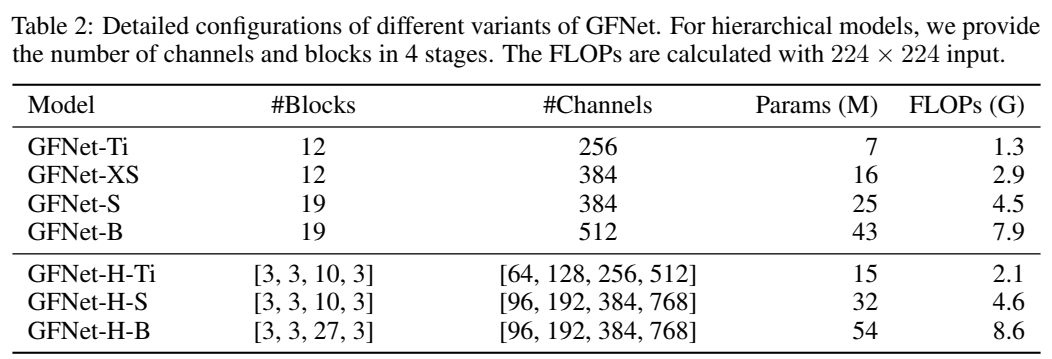
作者还根据 CNN 的分层架构模式设计了几种变体：

image-20230423144450779

Experiment

ImageNet

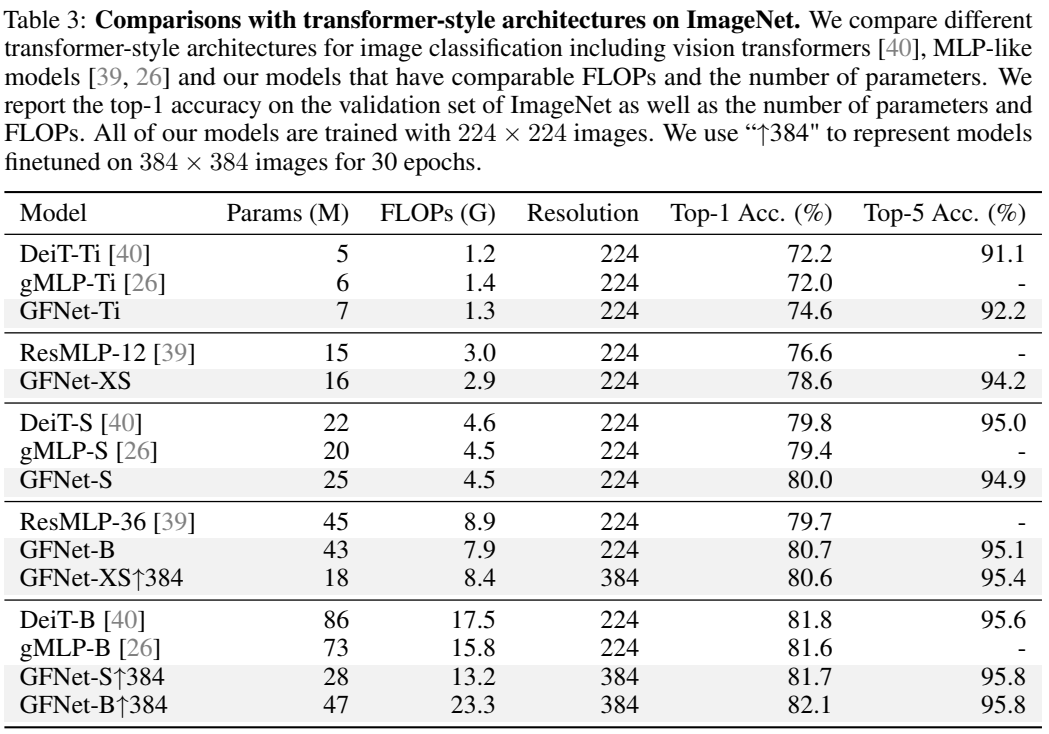
image-20230423144532948
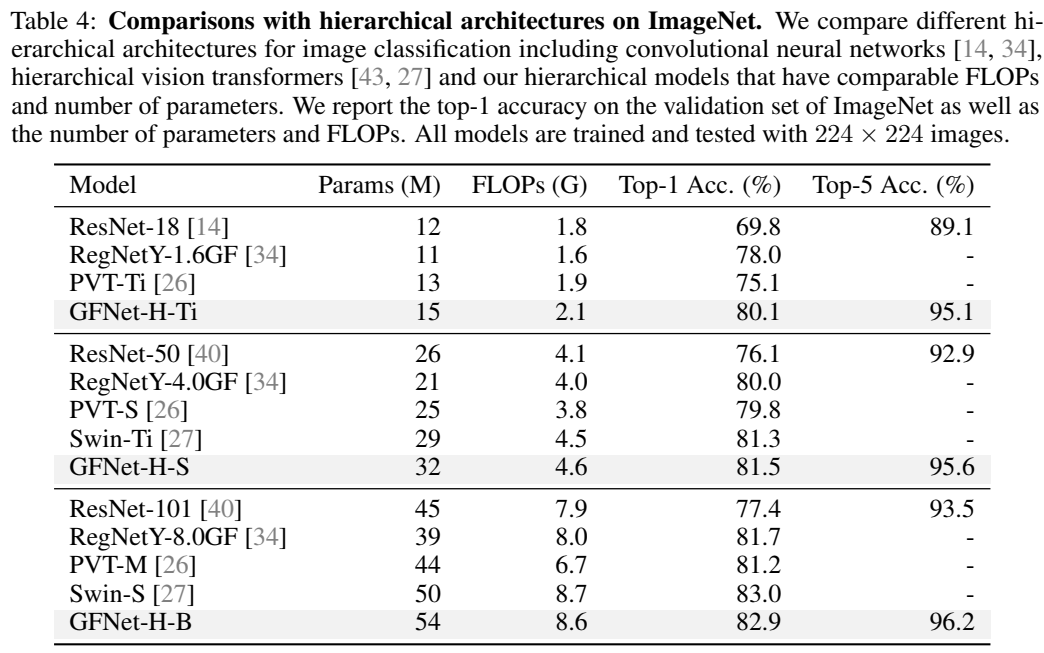
image-20230423144548297

迁移学习

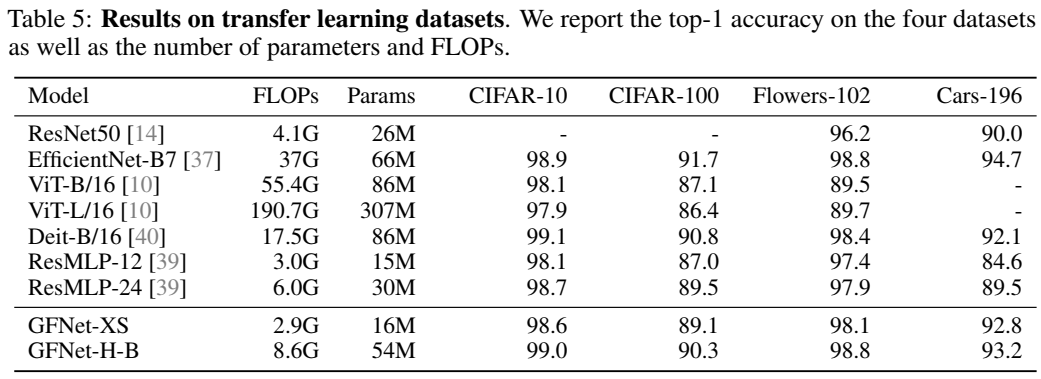
image-20230423144607101

效率对比

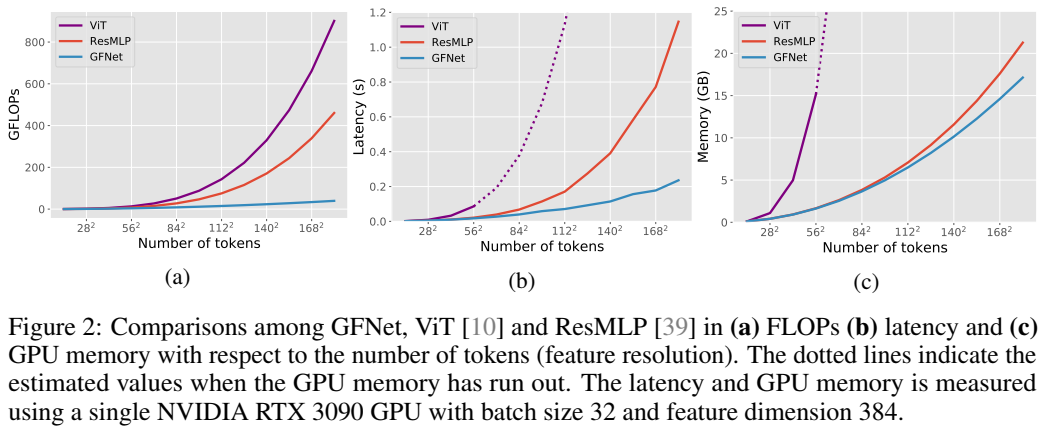
image-20230423144711986
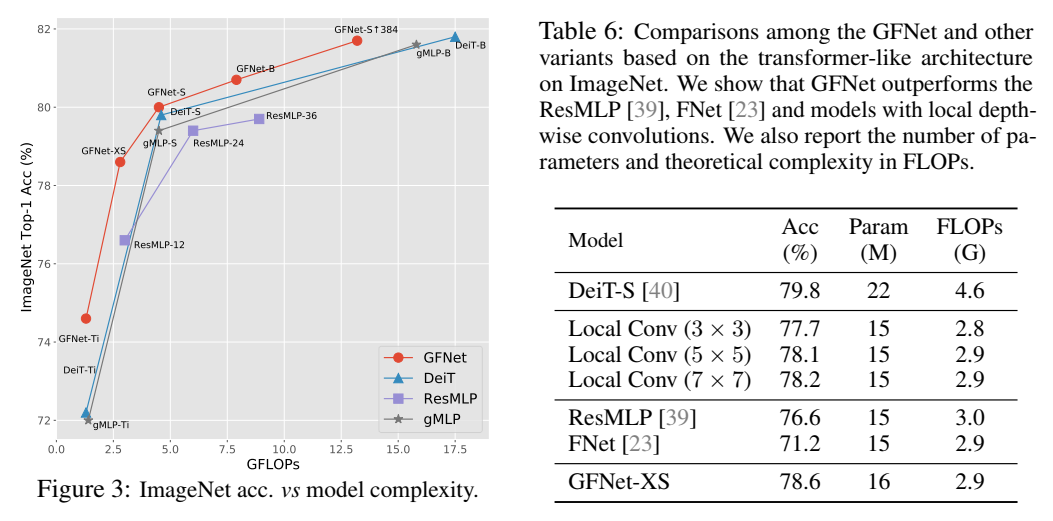
image-20230423144723996

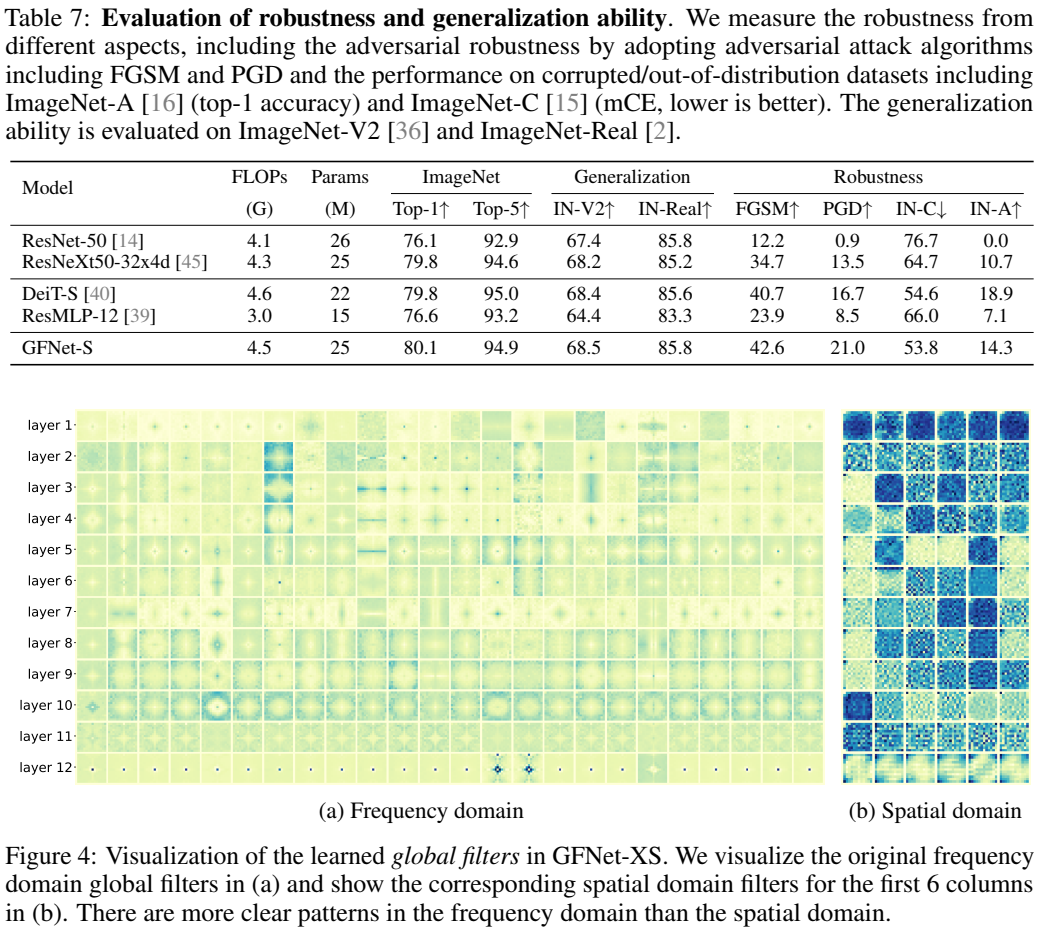
消融及可视化实验

image-20230423144748419

Conclusion

提出了全局滤波网络 GFNet，一种简单高效的结构。作者使用二维傅里叶变换和逆傅里叶变换以及一组可学习的全局滤波器来代替 Transformer 中的 self-attention 层，且效率更好。

Others

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
import torch
import torch.nn as nn

class GlobalFilter(nn.Module):
    def __init__(self, dim, h=14, w=8):
        super().__init__()
        self.complex_weight = nn.Parameter(torch.randn(h, w, dim, 2, dtype=torch.float32) * 0.02)

    def forward(self, x):
        B, H, W, C = x.shape
        x = torch.fft.rfft2(x, dim=(1, 2), norm='ortho')
        weight = torch.view_as_complex(self.complex_weight)
        x = x * weight
        x = torch.fft.irfft2(x, s=(H, W), dim=(1, 2), norm='ortho')
        return x

显然作者使用的是旧版的 pytorch 的 fft 函数库的函数，输出会多一个大小为 2 的维度，分别表示实部和虚部部分，而在新版的 fft 函数库中的函数输出的是复数类型的，所以处理起来更简单了。

如有错漏，欢迎指正！如果对你有帮助的话，请给我点个赞吧~

欢迎前往 我的博客 查看更多笔记

--- ♥ end ♥ ---

欢迎关注我呀~