小鲸鱼的梦境
0%

『论文笔记』PNP - Robust Learning from Noisy Labels by Probabilistic Noise Prediction

发表于 分类于 Valine：
本文字数： 6.3k 阅读时长 ≈ 6 分钟

Information

  • Title: PNP: Robust Learning from Noisy Labels by Probabilistic Noise Prediction
  • Author: Zeren Sun, Fumin Shen, Dan Huang, Qiong Wang, Xiangbo Shu, Yazhou Yao, and Jinhui Tang(姚亚洲老师团队工作)
  • Institution: 南京理工大学，成都科技大学
  • Year: 2022
  • Journal: CVPR
  • Source: OpenAccess, PDF, IEEE, Github
  • Cite: Zeren Sun, Fumin Shen, Dan Huang, Qiong Wang, Xiangbo Shu, Yazhou Yao, Jinhui Tang; Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), 2022, pp. 5311-5320
  • Idea: 通过网络以端到端的方法预测噪声类型从而选择性的对网络进行训练优化
1
2
3
4
5
6
7
8
@InProceedings{Sun_2022_CVPR,
    author    = {Sun, Zeren and Shen, Fumin and Huang, Dan and Wang, Qiong and Shu, Xiangbo and Yao, Yazhou and Tang, Jinhui},
    title     = {PNP: Robust Learning From Noisy Labels by Probabilistic Noise Prediction},
    booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
    month     = {June},
    year      = {2022},
    pages     = {5311-5320}
}

Abstract

噪声标签是深度学习中的一个问题，因为神经网络通常具备很强的拟合训练数据的问题，以往的方法通常通过样本选择的方法来划分样本，例如排序或阈值。该文章提出了一种称为概率噪声预测(PNP, Probabilistic Noise Prediction)的方法来建模噪声标签。总的来说，PNP 同时训练两个网络，一个预测类别标签，一个预测噪声类型，通过预测的标签噪声概率可以识别噪声样本并使用对应的优化目标，最终的优化目标是联合损失，包括分类损失，辅助约束损失，分布内一致性损失。

Introduction

在大规模数据集中因为各种原因总是不可避免的会有一些噪声标签，这对深度学习的模型性能会有影响，所以建立对噪声标签具有鲁棒性的模型是有意义的。

噪声标签通常有两种：开集和闭集。闭集噪声主要是已知的标签空间的的噪声标签，而开集则是已知标签空间之外的。简单理解就是，闭集是数据集的标签标错了，而开集则是一些不是训练集内类别的样本。闭集噪声样本是 ID (in-distribution)，开集噪声样本为 OOD(out-of-distribution)。

作者提出 PNP 的方法，同时训练两个网络，一个标签预测网络，一个噪声预测网络，噪声预测网络可以识别干净样本，ID样本、OOD样本。对噪声预测网络使用回归的方式进行优化，在预测-标签对和预测-预测对使用JS散度计算。最后对 ID 数据添加一致性约束。

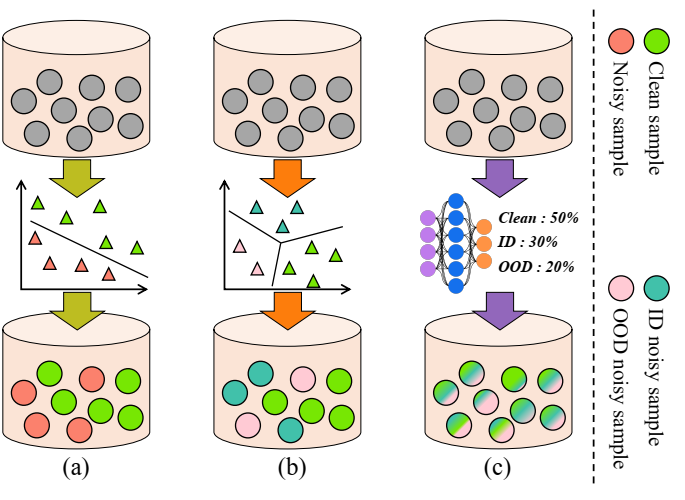
image-20230304154710237

上图 (a) 是早期的方法，只将样本分为干净样本和噪声样本，(b) 将噪声样本分为干净样本、ID样本、OOD样本，而 (c) 作者提出通过网络预测样本噪声概率。

该文章的贡献：

  1. 提出了对抗噪声的方法 PNP，可以在有噪声的数据中进行鲁棒学习
  2. PNP 采用辅助损失使得模型能预测样本的噪声类型，采用预测-标签对和预测-预测对之间的JS散度来近似真实噪声类型。此外，对分布内数据的不同视图之间的一致性进行约束，以增强识别能力
  3. 给出了两种样本寻找范式：PNP-Hard 和 PNP-soft，实验表明效果很好

Method

首先是常规的优化目标 \[ \mathcal{L}=\mathbb{E}_{\mathcal{D}}\left[l_{c e}\left(x_{i}, y_{i}\right)\right]=\frac{1}{N} \sum_{i=1}^{N} l_{c e}\left(x_{i}, y_{i}\right) \] 其中 \(x_i\) 是样本，\(y_i\) 是对应的标签（假设标签没有噪声都是对的），数据集有 \(N\) 样本 \(C\) 类，通过最下化经验损失优化： \[ l_{c e}\left(x_{i}, y_{i}\right)=-\sum_{c=1}^{C} y_{i}^{c} \log \left(p^{c}\left(x_{i}, \Theta\right)\right) \] \(\Theta\) 表示模型参数。

作者提出以端到端概率的方式直接对标签噪声建模，其中包含两个网络，一个是标签预测网络(LPN)，用于预测类别标签： \[ p\left(x_i\right)=\sigma\left(h\left(f\left(x_i, \Psi\right), \Phi_L\right)\right) \in \mathbb{R}^C \] 其中 \(\Phi_L\) 表示 LPN 预测头的参数，\(\Psi\) 表示 backbone 的参数， \(f(\cdot, \Psi)\) 和 \(h\left(\cdot, \Phi_L\right)\) 是二者的映射函数. \(\sigma(\cdot)\) 是 softmax 函数。另一个网络是噪声预测网络(noise predictor network, NPN)，用于识别噪声类型： \[ t\left(x_i\right)=\sigma\left(g\left(f\left(x_i, \Psi\right), \Phi_N\right)\right) \in \mathbb{R}^3, \] \(\Phi_N\) 是NPN的预测头， \(g\left(\cdot, \Phi_N \right)\) 是其映射函数，具体实现未是一个带有一个隐藏层的MLP网络，而 NPN 和 LPN 是共享 backbone 的。

对于干净样本使用交叉熵损失优化： \[ l_{\text {clean }}\left(x_i, y_i\right)=-\sum_{c=1}^C y_i^c \log \left(p_i^c\right)-\sum_{c=1}^C p_i^c \log \left(p_i^c\right) \] 对于 ID 样本，借鉴无监督一致性训练的方法，将强增强和弱增强输入网络然后对输出计算交叉熵损失： \[ l_{i d}\left(x_i\right)=l_{c e}\left(p\left(v_i^s\right), \varepsilon\left(p\left(v_i^w\right), \tau\right)\right) \] 其中 \[ \varepsilon(z, T)=\frac{\exp (z / T)}{\sum_{z^*} \exp \left(z^* / T\right)} . \] 对 OOD 样本也采用同样的处理方法 \[ l_{\text {ood }}\left(x_i\right)=l_{c e}\left(p\left(v_i^s\right), \varepsilon\left(p\left(v_i^w\right), 1 / \tau\right)\right) . \] 经验的设置 \(\tau = 0.1\) 使 ID 中的 \(\varepsilon\) 是锐化操作而 OOD 是扁平操作。 这么做的原因是对于 ID 样本，训练好的模型的预测结果比给定的结果更可靠一些，而对于 OOD 噪声因为是给定任务外的类别模型更容易混淆，所以将预测拟合到一个近似均匀分布，从而提高鲁棒性和泛化性。

但因为不知道标签是不是准确的，所以训练 NPN 网络是困难的，在这篇文章中，作者提出估计每个样本的噪声类型并用于训练 NPN 网络，具体来说，使用 JS 散度来估计每个样本是干净样本的概率： \[ \mathcal{Q}_i^{\text {clean }}=\mathcal{Q}^{\text {clean }}\left(x_i\right)=1-D_{J S}\left(p\left(v_i^w\right) \| y_i\right) \] 其中 \(D_{J S}(\cdot \| \cdot)\) 是 JS 散度函数。同样的，使用预测散度来估计样本是 OOD 的可能性 \(\mathcal{Q}^{\text {ood }}\)： \[ \mathcal{Q}_i^{\text {ood }}=\mathcal{Q}^{\text {ood }}\left(x_i\right)=D_{J S}\left(p\left(v_i^w\right) \| p\left(v_i^{w^{\prime}}\right)\right), \] 其中 \(v_i^{w^{\prime}}\) 表示 \(x_i\) 的另一个弱增强视图。 随后采用下面的辅助约束损失来优化 NPN： \[ l_{\text {aux }}\left(x_i\right)=\left|\mathcal{P}_i^{\text {clean }}-\mathcal{Q}_i^{\text {clean }}\right|+\left|\mathcal{P}_i^{\text {ood }}-\mathcal{Q}_i^{\text {ood }}\right| \] 因为对 OOD 样本使用了预测散度，作者提对 ID 样本添加一致性正则化约束： \[ l_{\text {cons }}\left(x_i\right)=D\left(p\left(v_i^w\right) \| p\left(v_i^{w^{\prime}}\right)\right)+D\left(p\left(v_i^{w^{\prime}}\right) \| p\left(v_i^w\right)\right) \] \(D\) 表示 KL 散度。一致性正则化不仅增强了表征学习，而且使模型能够更好地区分 ID 噪声和 OOD 噪声。

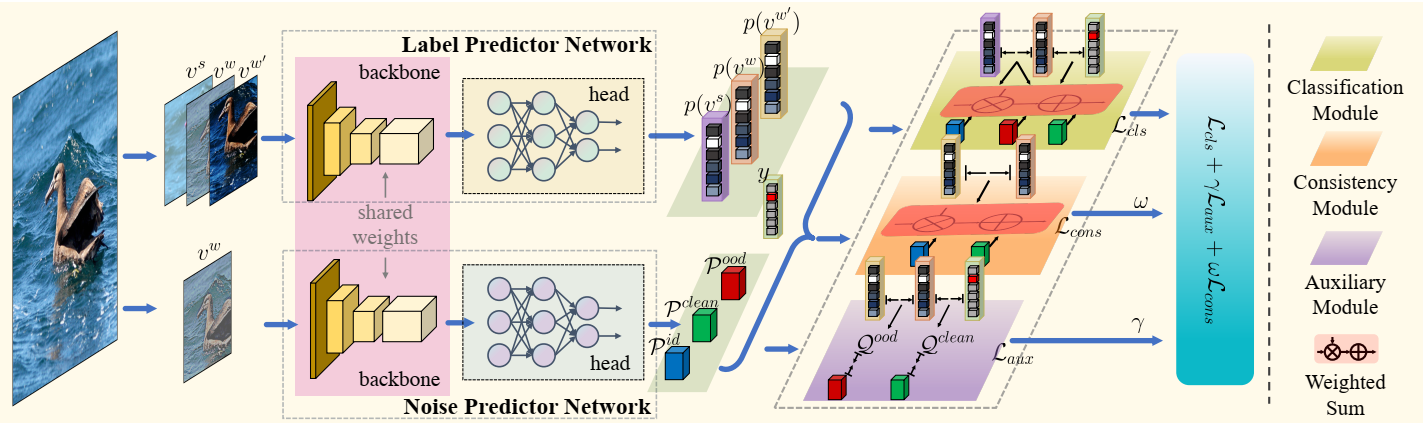
image-20230304164139595

PNP 的整体框架示意图：输入样本并行的输入到两个网络 LPN 和NPN，NPN预测样本是干净样本、ID 样本、OOD 样本的概率，而输入 LPN 网络的是两个强增强和一个弱增强的视图，从而得到三个标签预测。随后根据噪声类型和选择范式计算分类损失。在辅助模块通过近似噪声类型计算约束损失。一致性损失通过不同视图之间的预测一致性计算得到。

NPN 的训练分两步。预热期先使用原始标签训练一小段时间，随后使用端到端的方法进行训练： \[ \mathcal{L}=\mathcal{L}_{\text {cls }}+\gamma \mathcal{L}_{a u x}+\omega \mathcal{L}_{\text {cons }} \] \(\gamma\) 和 \(\omega\) 是平衡损失项。

在该文章中给出了两种选择范式：软选择和硬选择，不同的范式有不同的损失函数，对于硬选择： \[ \left\{\begin{aligned} \mathcal{L}_{\text {cls }} & =\mathbb{E}_{\mathcal{D}}\left[\mathbb{1}_{\mathcal{P}_i^{\text {clean }} \geq \max \left(\mathcal{P}_i^{i d}, \mathcal{P}_i^{\text {ood }}\right)} l_{\text {clean }}\left(x_i, y_i\right)\right. \\ & +\mathbb{1}_{\mathcal{P}_i^{i d}>\max \left(\mathcal{P}_i^{\text {clean }}, \mathcal{P}_i^{\text {ood }}\right)} l_{i d}\left(x_i\right) \\ & \left.+\mathbb{1}_{\mathcal{P}_i^{\text {ood }}>\max \left(\mathcal{P}_i^{i d}, \mathcal{P}_i^{\text {clean }}\right)} l_{\text {ood }}\left(x_i\right)\right] \\ \mathcal{L}_{\text {cons }} & =\mathbb{E}_{\mathcal{D}}\left[\mathbb{1}_{\mathcal{P}_i^{\text {ood }}<\max \left(\mathcal{P}_i^{i d}, \mathcal{P}_i^{\text {clean }}\right)} l_{\text {cons }}\left(x_i\right)\right] \end{aligned}\right. \] \(\mathbb{1}_A\) 是指标函数如果 \(\mathrm{A}\) 是 true 为 1，否则为 0。

而软选择是对样本损失进行加权得到最终损失： \[ \left\{\begin{aligned} \mathcal{L}_{\text {cls }}= & \mathbb{E}_{\mathcal{D}}\left[\mathcal{P}_i^{\text {clean }} l_{\text {clean }}\left(x_i, y_i\right)\right. \\ & \left.+\mathcal{P}_i^{i d} l_{i d}\left(x_i\right)+\mathcal{P}_i^{\text {ood }} l_{\text {ood }}\left(x_i\right)\right] \\ \mathcal{L}_{\text {cons }}= & \mathbb{E}_{\mathcal{D}}\left[\left(\mathcal{P}_i^{\text {clean }}+\mathcal{P}_i^{i d}\right) l_{\text {cons }}\left(x_i\right)\right] \end{aligned}\right. \] 硬选择相对更信任噪声预测结果，导致过拟合，而软选择可能更会出现欠拟合的问题。经验来看，噪声不显著时硬选择好一些，而噪声严重时软选择好一些。

Experiment

简单看看论文中的一些实验结果叭：

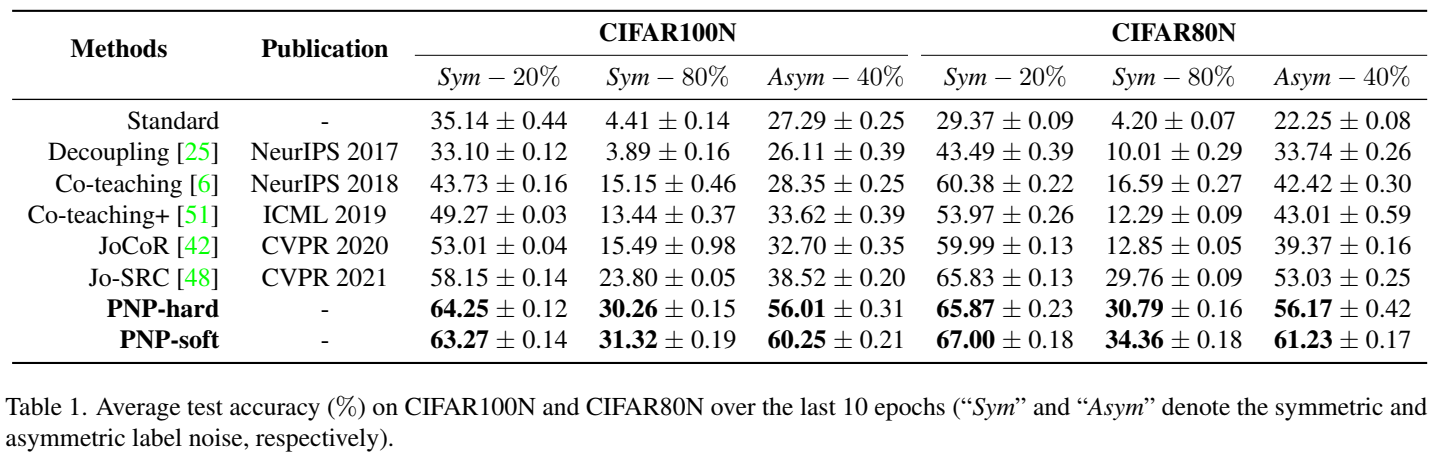
首先是合成噪声数据集的结果

image-20230304170513515

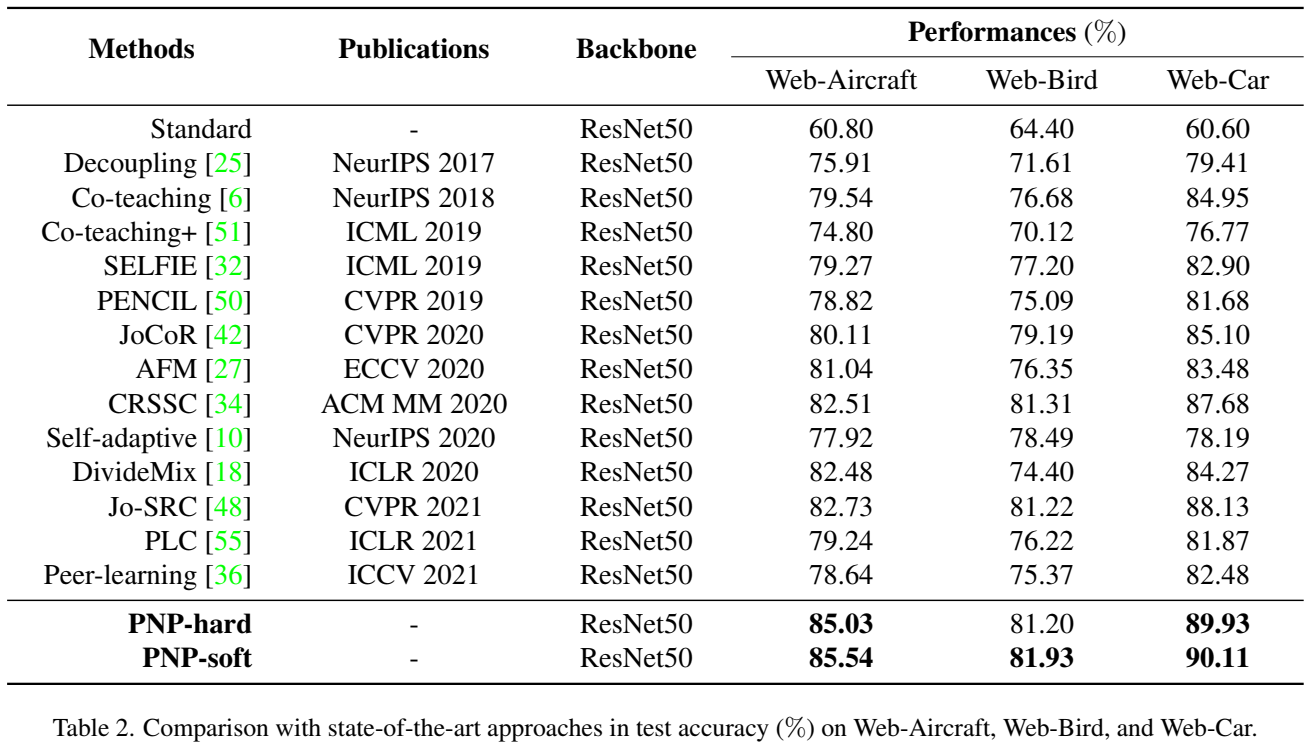
接下来是真实世界噪声数据集

image-20230304170645312

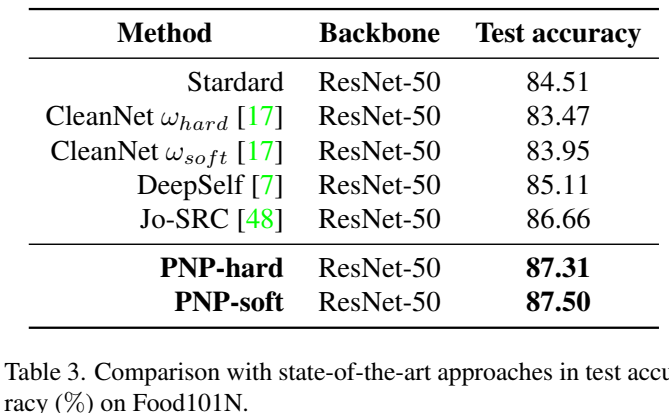
image-20230304170719354

最后是一些消融实验

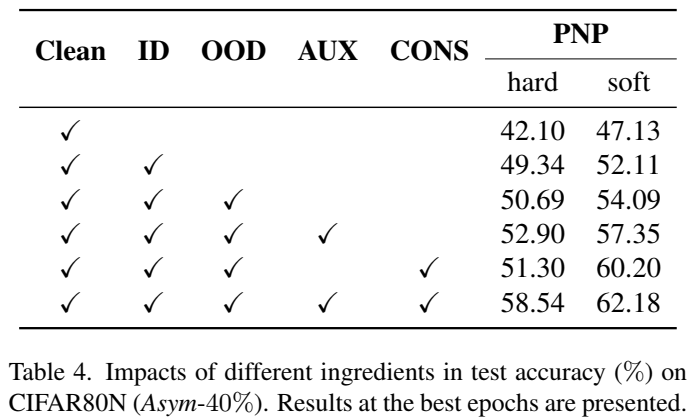
image-20230304170736932

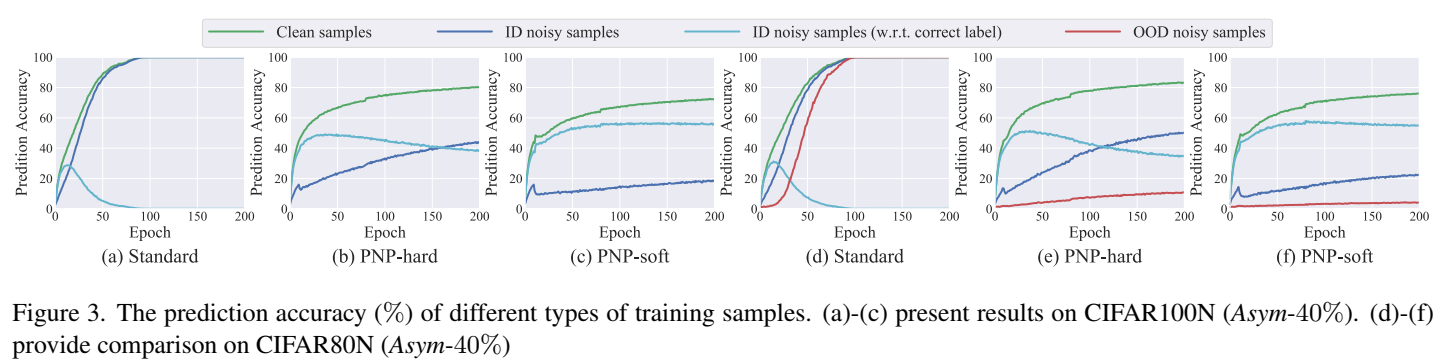
image-20230304170749113

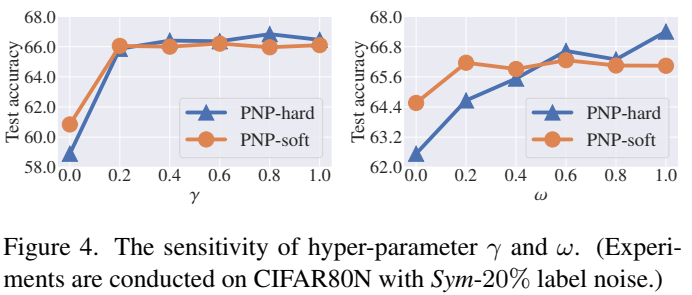
image-20230304170756007

Conclusion

在该文章中，作者专注于从现实世界(开集)噪声标签中学习的挑战。为了减轻它们的负面影响，作者提出了一种简单而有效的方法，称为PNP，以端到端概率的方式对标签噪声建模。PNP遵循样本选择范式，但绕过了选择阈值的要求，这是难以调优和依赖于数据集的。具体来说，PNP并行训练两个网络，能够同时预测类别标签(即LPN)和噪声类型(即NPN)。此外，采用回归任务优化NPN，采用一致性正则化增强识别能力。最后，作者评估了PNP的两种选择范式(即PNP-硬和PNP-软)。在合成数据集和真实数据集上的一系列实验结果证明了方法的有效性和优越性。

如有错漏，欢迎指正！如果对你有帮助的话，请给我点个赞吧~

欢迎前往 我的博客 查看更多笔记

--- ♥ end ♥ ---

欢迎关注我呀~