小鲸鱼的梦境
0%

『论文笔记』Semantic Image Synthesis With Spatially-Adaptive Normalization

发表于 分类于 Valine：
本文字数： 4.2k 阅读时长 ≈ 4 分钟

Information

  • Title: Semantic Image Synthesis With Spatially-Adaptive Normalization
  • Author: Taesung Park, Ming-Yu Liu, Ting-Chun Wang, Jun-Yan Zhu
  • Institution: UC Berkeley, NVIDIA, MIT CSAIL
  • Year: 2019
  • Journal: CVPR
  • Source: Open access, Github
  • Idea: 通过空间自适应归一化计算 norm 层的仿射变换参数
1
2
3
4
5
6
7
@InProceedings{Park_2019_CVPR,
author = {Park, Taesung and Liu, Ming-Yu and Wang, Ting-Chun and Zhu, Jun-Yan},
title = {Semantic Image Synthesis With Spatially-Adaptive Normalization},
booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
month = {June},
year = {2019}
}

Abstract

对于输入布局语义来合成逼真图像的网络，作者认为常规的 Normalization 层会“洗掉”语义信息，所以提出了使用输入布局来在 Normalization 层通过空间自适应来建模激活。

Introduction

作者使用的合成网络是基于 GAN 的对抗生成式网络，使用带有语义的 mask 图像来生成逼真的图片（从后面实验结果来看其实就是图像分割的逆过程）。

作者将 BN,IN,LN,WN 归类为无条件的 Normalization 因为它们不依赖于额外的数据，而 CBN(Conditional BatchNorm), AdaIN 等被归类为条件 Normalization，它们需要一些额外数据，和无条件的 Normalization 类似，先将其 norm 到 0 均值和单位方差，随后做一个仿射变换，但仿射变换的参数是由额外数据得到的。

作者提出的方法是针对空间信息的仿射变换，有另外一篇类似方法的论文：Recovering realistic texture in image super-resolution by deep spatial feature transform.

Method

作者提出的方法 SPADE 如下所示

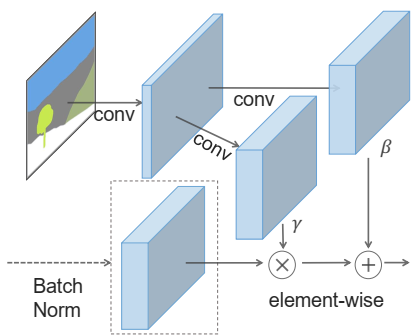
image-20221021104613739

数学表达式为： \[ \gamma^i_{c,y,x}(\mathbf{m}) \frac{h^i_{n,c,y,x}-\mu^i_c}{\sigma^i_c} + \beta^i_{c,y,x}(\mathbf{m}) \] 其中 \((n\in N,c \in C^i,y \in H^i,x \in W^i)\)，\(\gamma, \beta\) 在传统方法中是可学习参数，而这里使用函数形式表示将 \(m\) (\(m\) 是输入的 mask 语义图像)的一个映射，具体实现是一个简单的两层卷积网络 \[ \begin{align} \mu^i_c &= \frac{1}{N H^i W^i}\sum_{n,y,x} h^i_{n,c,y,x}\\ \sigma^i_c &= \sqrt{\frac{1}{N H^i W^i}\sum_{n,y,x} \Big( (h^i_{n,c,y,x})^2 - (\mu^i_c)^2 \Big) }. \end{align} \] 从 \(m\) 提取的特征是空间不变的，如果吧 \(m\) 换成一个风格图片，那就和 AdaIn 是等价的了。

为什么 SPADE 有用呢？作者的解释是想不通用的Normalization层它能更好的保留语义信息，换而言之，就是如 IN 这样的规范层会把语义信息“洗掉”，作者举了一个极端一点的例子语义图像是完全相同的像素点，经过 IN 以后语义信息完全丢失了。相反，SPADE生成器中的语义图像是通过空间自适应机制的，没有规范化，只有来自前一层的激活才会被规范化。因此，SPADE生成器可以更好地保存语义信息。它具有规范化的好处，又不会丢失语义输入信息。

Detail

网络的一些细节

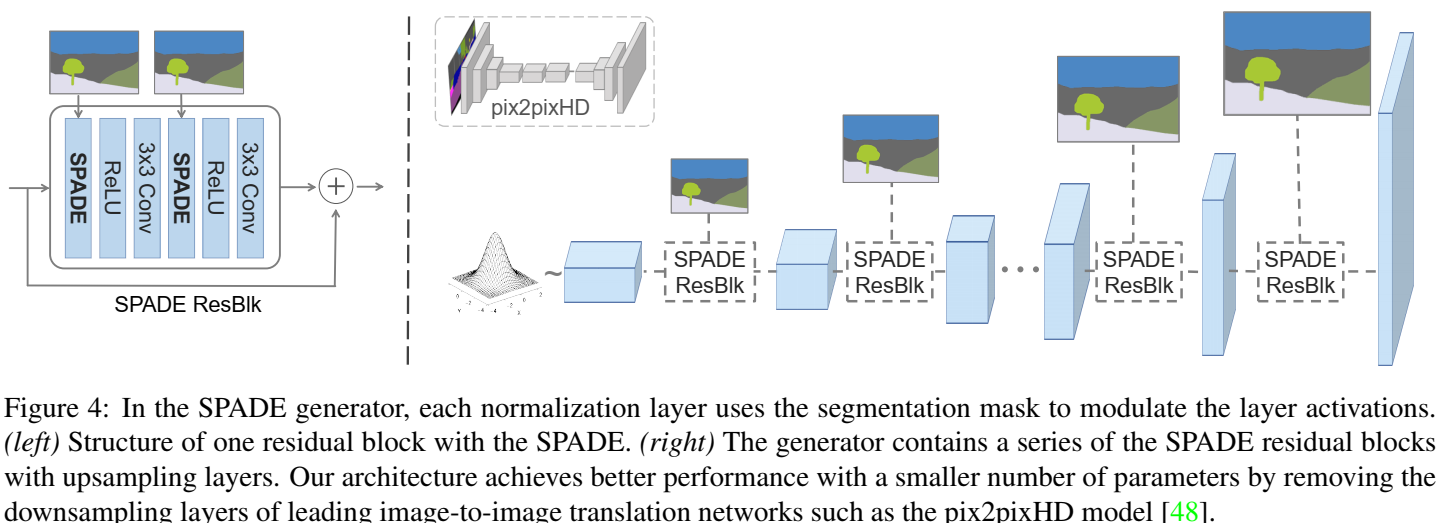
image-20221021141534510

Experiment

略过，论文很多图，总的来说比以往的方法效果好一些，但一些精细的图像还是挺假的。

image

Conclusion

就是提出了空间自适应正则化方法，用于正则化层的仿射变换，使得模型能合成更真实的图像

Code

看看代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
# Creates SPADE normalization layer based on the given configuration
# SPADE consists of two steps. First, it normalizes the activations using
# your favorite normalization method, such as Batch Norm or Instance Norm.
# Second, it applies scale and bias to the normalized output, conditioned on
# the segmentation map.
# The format of |config_text| is spade(norm)(ks), where
# (norm) specifies the type of parameter-free normalization.
#       (e.g. syncbatch, batch, instance)
# (ks) specifies the size of kernel in the SPADE module (e.g. 3x3)
# Example |config_text| will be spadesyncbatch3x3, or spadeinstance5x5.
# Also, the other arguments are
# |norm_nc|: the #channels of the normalized activations, hence the output dim of SPADE
# |label_nc|: the #channels of the input semantic map, hence the input dim of SPADE
class SPADE(nn.Module):
    def __init__(self, config_text, norm_nc, label_nc):
        super().__init__()

        assert config_text.startswith('spade')
        parsed = re.search('spade(\D+)(\d)x\d', config_text)
        param_free_norm_type = str(parsed.group(1))
        ks = int(parsed.group(2))

        if param_free_norm_type == 'instance':
            self.param_free_norm = nn.InstanceNorm2d(norm_nc, affine=False)
        elif param_free_norm_type == 'syncbatch':
            self.param_free_norm = SynchronizedBatchNorm2d(norm_nc, affine=False)
        elif param_free_norm_type == 'batch':
            self.param_free_norm = nn.BatchNorm2d(norm_nc, affine=False)
        else:
            raise ValueError('%s is not a recognized param-free norm type in SPADE'
                             % param_free_norm_type)

        # The dimension of the intermediate embedding space. Yes, hardcoded.
        nhidden = 128

        pw = ks // 2
        self.mlp_shared = nn.Sequential(
            nn.Conv2d(label_nc, nhidden, kernel_size=ks, padding=pw),
            nn.ReLU()
        )
        self.mlp_gamma = nn.Conv2d(nhidden, norm_nc, kernel_size=ks, padding=pw)
        self.mlp_beta = nn.Conv2d(nhidden, norm_nc, kernel_size=ks, padding=pw)

    def forward(self, x, segmap):

        # Part 1. generate parameter-free normalized activations
        normalized = self.param_free_norm(x)

        # Part 2. produce scaling and bias conditioned on semantic map
        segmap = F.interpolate(segmap, size=x.size()[2:], mode='nearest')
        actv = self.mlp_shared(segmap)
        gamma = self.mlp_gamma(actv)
        beta = self.mlp_beta(actv)

        # apply scale and bias
        out = normalized * (1 + gamma) + beta

        return out

初始化的部分挺多的，但实际上在 forward 部分流程很清楚，就是

  1. 先做一个无参数的 Normalize 的操作，这里看可以是不带仿射变换的 IN 或 BN
  2. 基于 segmap 计算仿射变换的 \(\gamma\) 和 \(\beta\), 具体计算可以看前面的，都是基于二维卷积的操作
  3. 将 \(\gamma\) 和 \(\beta\) 应用到仿射变换操作

如果对你有帮助的话，请给我点个赞吧~

欢迎前往 我的博客 查看更多笔记

--- ♥ end ♥ ---

欢迎关注我呀~