小鲸鱼的梦境
0%

『论文笔记』Subspace Adversarial Training

发表于 更新于 分类于 Valine：
本文字数： 5.7k 阅读时长 ≈ 5 分钟

Information

  • Title: Subspace Adversarial Training
  • Author: Tao Li, Yingwen Wu, Sizhe Chen, Kun Fang, Xiaolin Huang
  • Institution: 上海交通大学(sjtu.edu.cn)
  • Year: 2022
  • Journal: CVPR 2022
  • Source: CVPR 2022 open access, PDF, supplemental
  • Idea: Sub-AT, 即在子空间中进行 AT 来避免过拟合的问题
1
2
3
4
5
6
7
8
@InProceedings{Li_2022_CVPR,
    author    = {Li, Tao and Wu, Yingwen and Chen, Sizhe and Fang, Kun and Huang, Xiaolin},
    title     = {Subspace Adversarial Training},
    booktitle = {Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR)},
    month     = {June},
    year      = {2022},
    pages     = {13409-13418}
}

Abstract

  1. 单步对抗训练(Single-step AT) 非常有效并且鲁棒，但有个很严重的问题就是会出现严重的灾难过拟合现象。
  2. 提出了一种新的优化方法 Subspace AT, 约束 AT 在一个仔细选取的子空间内，不但可以解决过拟合，还能显著提高鲁棒性。
  3. 揭示了快速增加的梯度和过拟合的关系。

Introduction

对抗训练 (AT) 旨在最小化模型对对抗样本的攻击的风险，能有效提高深度神经网络的鲁棒性。给定具有参数 \(w\) 的神经网络 \(f(x, w)\), AT 的优化目标是 \[ \min_\mathbf{w} \mathbb{E}_{(\mathbf{x},y)\sim \mathcal{D}} \left[ \max_{\delta \in \mathcal{B}(\mathbf{x}, \epsilon)} \mathcal{L} \left(f(\mathbf{x}+\delta, \mathbf{w}),y\right) \right] \] 其中 \(\mathcal{B}(\mathbf{x}, \epsilon)\) 表示半径为 \(\epsilon\) 的归一化球(norm ball, 可以理解为一个单位球形空间)。AT 的关键是通过生成对抗样本来进行训练，目前最有效的生成对抗样本的方法是快速梯度标志法(fast gradient sign method, FGSM) \[ \mathbf{x}^{\rm adv} = \mathbf{x} + \epsilon \cdot \mathrm{sgn} \left(\nabla_\mathbf{x} \mathcal{L} (f(\bf x,\bf w), y)\right). \] 因为对抗样本是通过一步生成的，所以对应的 AT 也称为 单步对抗训练(single-step AT).

Fig. 1

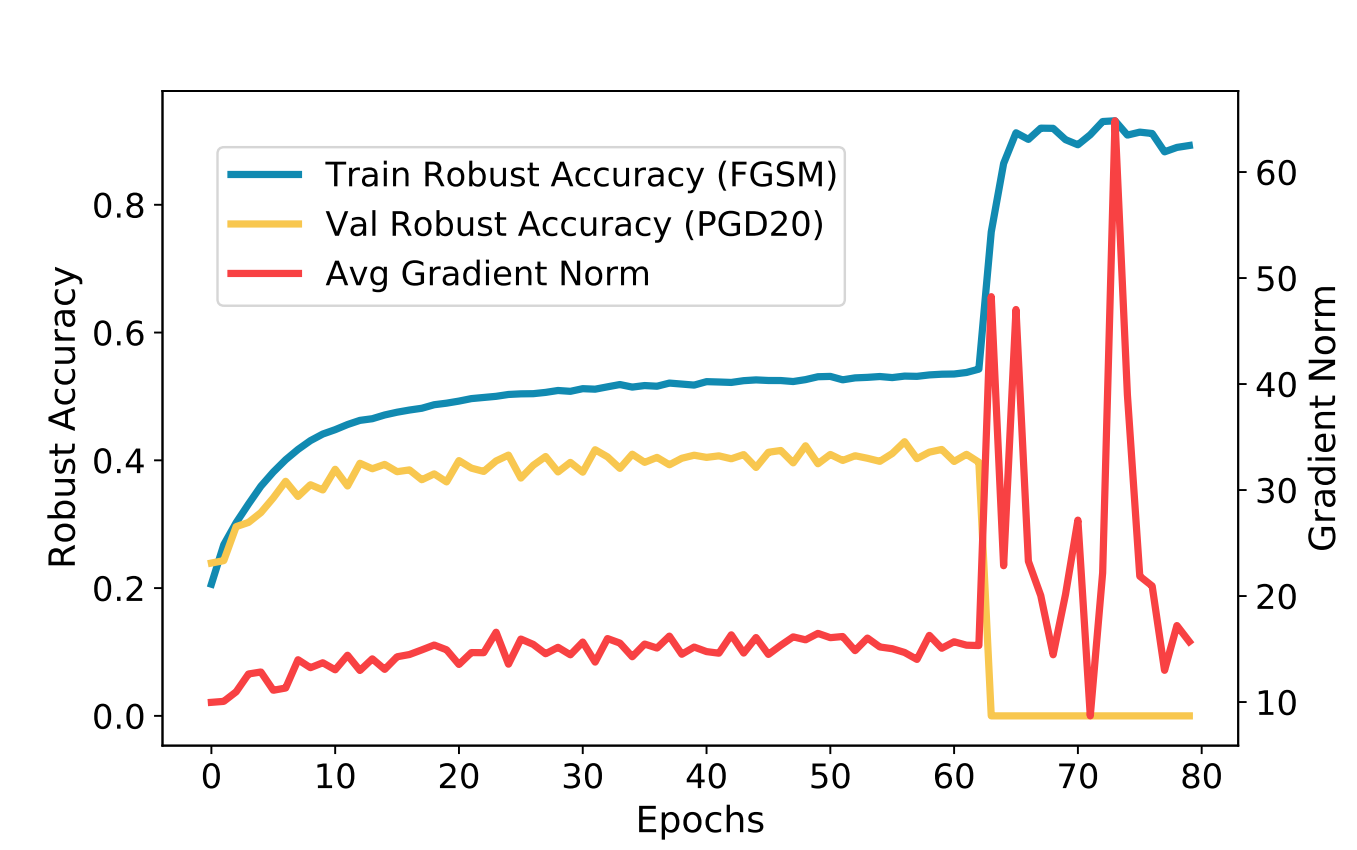
图一显示了灾难过拟合(catastrophic overfitting)现象，即使用 FGSM 训练鲁棒性一直保持增加，但在使用 PGD 的验证集上突然降低到 0. 一种解决方案是使用精心设计的学习率规则和适当的正则化, 这种方法非常依赖特殊设计的学习率规则，对于不同的任务需要小心的进行调整, 另一种方案是生成更精细的对抗样本。

  • [1] 提出添加随机步(random step) 到 FGSM 并引入循环学习率[2].
  • [3] 提出了一种名为 GradAlign 的正则换方法来提高单步 AT 解法的质量
  • [4] 建议确认独立于对抗方向的内间距并搜寻合适的步长
  • 传统的多步 AT 方法 PGD AT 也能避免灾难过拟合

接下来作者探究了灾难过拟合发生的原因：注意到在第 64 个 epochs 的时候发生了灾难过拟合，但训练鲁棒性仍然保存在稳定状态，考察其梯度范数 \(\left \| \frac{1}{n} \sum_{i=1}^n \nabla_{\bf w} \mathcal{L} (f(\bf x_i^{\rm adv},\bf w), y) \right \|_{2}\)，这有两种可能，一是每个样本的梯度都很小，二是样本梯度并不收敛，但彼此之间相互抵消导致最后结果相对稳定。于是作者探究了每个样本的平均梯度范数(\(\frac{1}{n} \sum_{i=1}^n \left \| \nabla_{\bf w} \mathcal{L} (f(\bf x_i^{\rm adv},\bf w), y) \right \|_{2}\)), 即红线所表示的，在过拟合前，平均范数都保持在稳定状态，但在发生过拟合现象的时候突然增大了，此时梯度平衡被打破了，即网络试图拟合所有样本，这是典型的过拟合。

由于过拟合是因为大的梯度波动导致的，作者受到启发提出通过控制那些巨大的梯度来预防过拟合。具体方法是限制梯度下降从原本的整个参数空间限制到一个子空间，以此限制梯度的剧烈变化。但关键是如何在子空间的限制下保证网络的性能，[5] 指出在一个子空间中优化是可以保持网络性能不下降的，基于上述观点，作者提出了 Sub-AT (Subspace Adversarial Training) 即如何确定一个有效的子空间并在其中进行对抗训练。

Single-step AT

multi-step AT

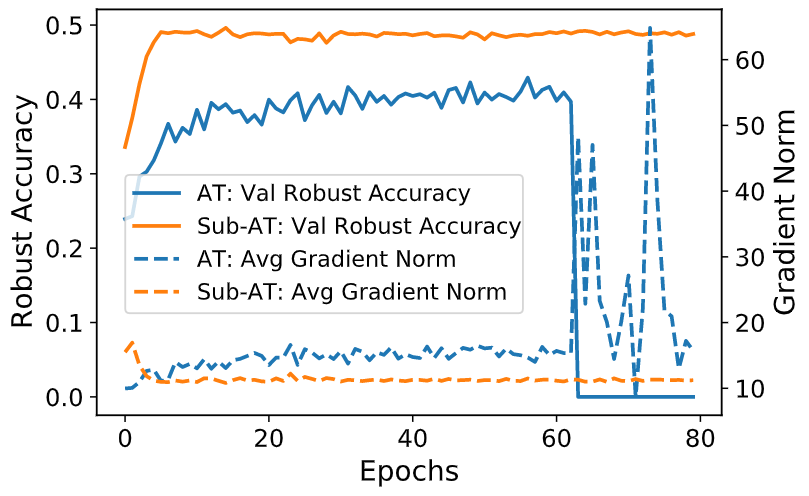
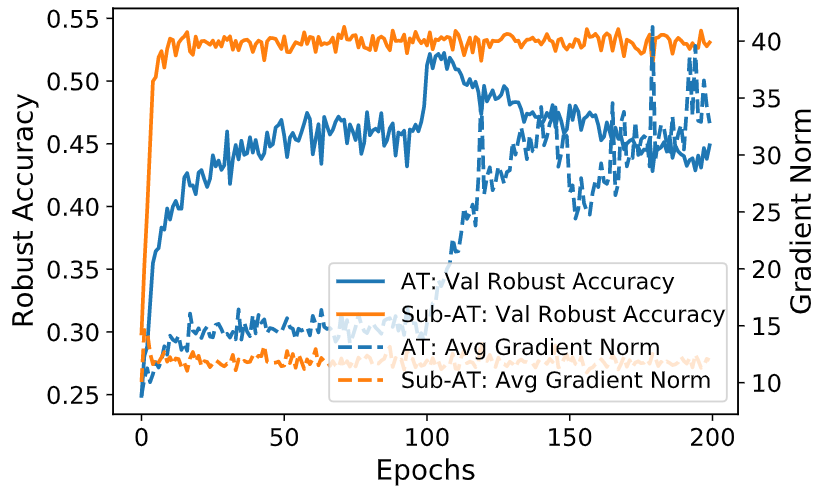
上面两幅图分别展示了 Sub-AT 在 单步和多步对抗攻击下的训练过程，从图中可以看到梯度范数被限制在了一个很低的范围，鲁棒性有显著提高，成功解决了灾难过拟合的问题。

总的来说：

  • 从优化的角度研究了单步对抗训练中的 灾难过拟合 并首次提出了每个样本快速增加的梯度与过拟合的联系，这种联系也可以拓展到多步对抗训练的 鲁棒过拟合.
  • 提出了 Sub-AT, 将 AT 限制在一个仔细选择的子空间以此控制梯度的增加。该方法解决了多种过拟合问题，显著提高了鲁棒性，并克服了学习率敏感的问题。同时还很容易联合其他 AT 方法一起使用。
  • Sub-AT 效果很好，在单步 AT 达到了 SOTA.

对抗训练

对抗训练是指在训练时添加对抗扰动来提高神经网络对抗对抗样本的鲁棒性。根据生成对抗样本时梯度传播次数，对抗训练分为单步对抗训练(Single-step AT)和多步对抗训练(Multi-step AT). 单步对抗训练更简单，多步对抗训练因为生成的对抗样本更强所以效果更好些，但多步的计算代价更高。

对抗训练中的过拟合

两种对抗训练的方法都存在过拟合的问题，例如灾难过拟合(catastrophic overfitting) [1]和鲁棒过拟合(robust overfitting) [6]. 其表现就是在训练过程中验证集的鲁棒性突然急剧下降，很多研究者通过设计精妙的学习率计划(lr_scheduler)或适当的正则化系列来解决这个问题。

在子空间中训练

已经有许多工作探究了神经网络训练中的低维度特征。[7] 开创性的提出通过随机投影的方法获得 90% 性能所需维度远远低于原始参数维度。[8] 提出动态的提取低维子空间进行训练，该论文使用了类似的方法。

原文中注释掉的部分大概说了下原理：所谓动态提取是指找最有效的方向进行投影而不是随机投影，以此在最大程度保留性能的基础上大大降低了维度，从而有效控制梯度范数

Method

分析灾难过拟合

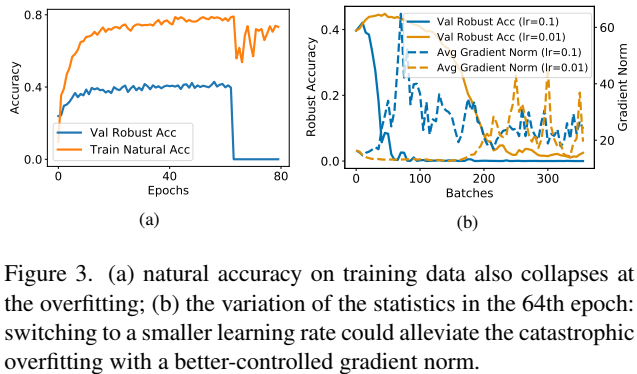
Figure3

作者认为灾难过拟合发生的原因是网络在不断在训练样本中捕获对抗信息，但对抗信息是使用 PGD 攻击生成的，是不断变化的，所以很难捕获，所以导致了网络不断大幅度波动并且鲁棒性和准确率都大幅度降低。

作者研究了 Fast AT 对抗 PGD-20 攻击时的鲁棒准确率并记录了每个样本的梯度平均范数，结果如图 1 所示。过拟合的发生与梯度的突增时机一致，说明正是梯度突然增加导致 了训练的巨大波动。在后续的研究中，作者发现

  • 过拟合与与平均梯度范数增加高度相关，巧妙的选择学习率能有效抑制梯度增加，这种方法拓展就是自适应启发式学习率
  • 想要避免灾难过拟合，就要控制平均梯度范数的增长

控制梯度爆炸

作者的主要想法是将对抗训练时梯度下降从整个参数空间限制到一个低维子空间，以此来抑制梯度的增加。首先要考虑的是如何获得这样的一个能保持 AT 性能的子空间：[8] 提出了一种算法 DLDR, 能有效的从训练路径中提取一个低维的子空间，其包含了两步：

  1. 在常规训练中采集模型检测点 \(\{\mathbf{w}_1,\mathbf{w}_2,\dots,\mathbf{w}_t\}\), 要求将模型参数与长度为 \(N\) 的向量 \(\mathbf{w}_i\) 对齐
  2. 对对齐的参数矩阵 \(\left [ \mathbf{w}_1,\mathbf{w}_2,\dots,\mathbf{w}_t\right ]\) 执行奇异值分解(SVD)获取维度为 \(d\) 的正交子空间 \([\mathbf{u}_1,\mathbf{u}_2,\dots,\mathbf{u}_d]\)

Sub-AT 采用 DLDR 的方法在出现过拟合现象前采样，随后回滚到初始化的检查点将梯度投影到子空间。

Algorithm

一些细节：

  • 采样策略：每个 epoch 均匀采样两次，并且尽量在过拟合之前的效果最好的一些epoch进行采样
  • Sub-AT 在实验中证明了对学习率不敏感，所以可以不需要 lr scheduler，将学习率设定为常数即可, 并且可以将 lr 设置为大一点的数值来让训练更快收敛

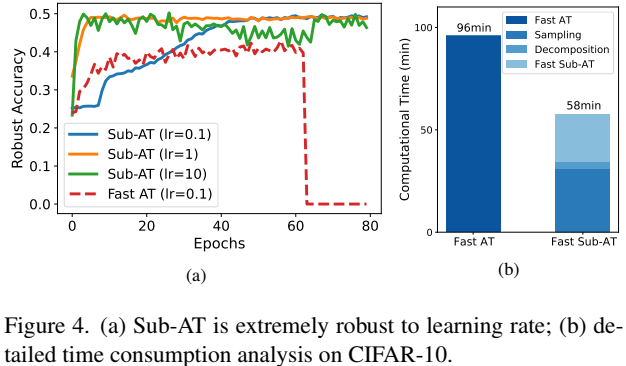
lr robust and detail time

计算分析: Sub-AT 包含两个部分，DLDR 和 子空间训练。其中 DLDR 也包括两个部分——采样和分解，分解的时间复杂度相对采样而言不值一提。而子空间训练的复杂度与表征的 AT 是一样的

Experiment

通过实验，先证明了在单步 AT 中能解决过拟合的问题并达到了 SOTA, 其次在更大的步数和更大的半径都能提高鲁棒性。

一篇很不错的关于对抗攻击和防御的综述：https://www.huxiu.com/article/434080.html

  • 数据集：CIFAR10/100, Tiny-ImageNet, 训练集按 9:1 的比例划分为训练集和验证集
  • 对抗攻击：使用了两种经典的对抗扰动, 半径 \(\epsilon=8/255\) 的 \(\ell_\infty\) 范数和 半径 \(\epsilon=128/255\) 的 \(\ell_2\) 范数。
  • lr_scheduler 使用了三种
    • cyclic
    • piecewise
    • constant
  • batch size 为 128, SGD optimizer, 附带 0.9 动量和 \(10^{-4}\) 权重衰减
  • 数据增强：4像素填充，随机裁剪，水平翻转
  • 测试独立重复五次，记录误差范围（很小）

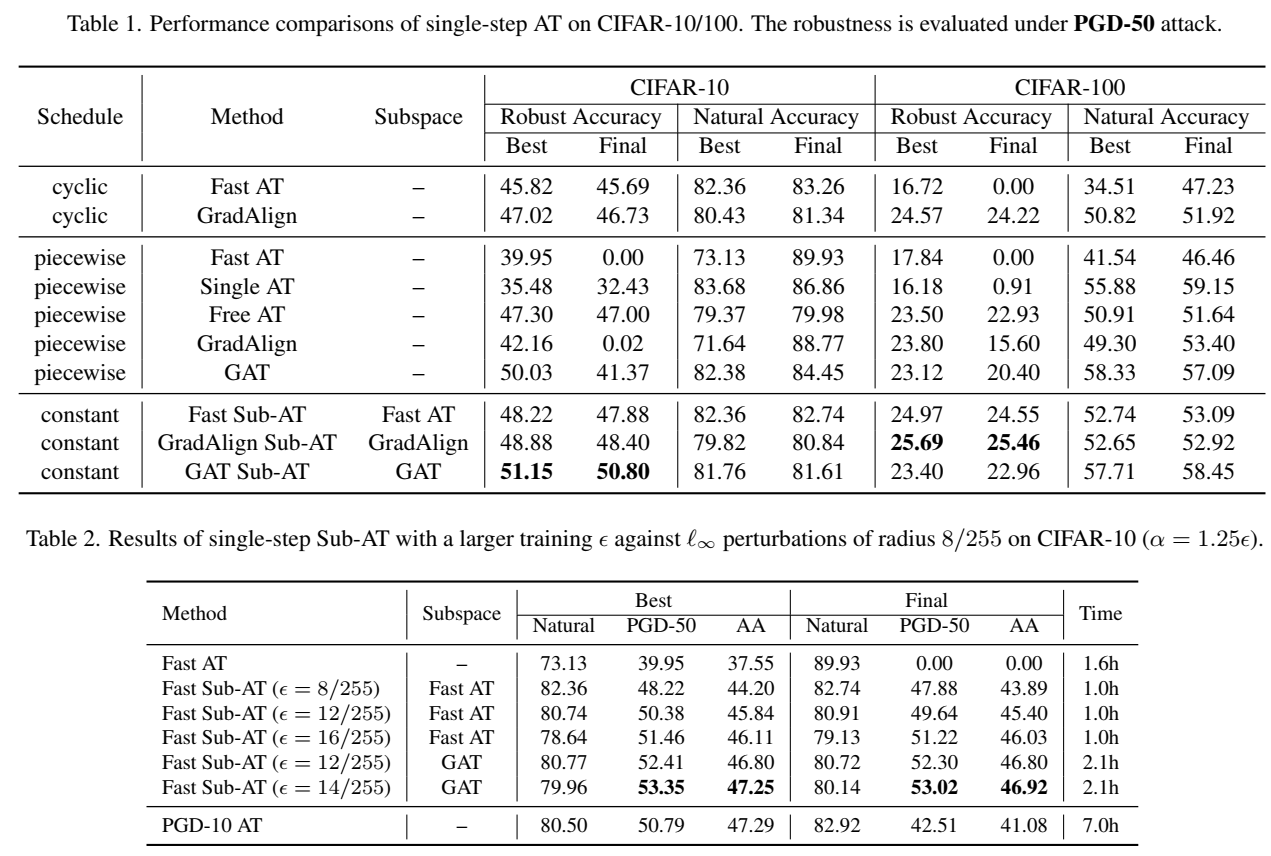
experiment

t3t4

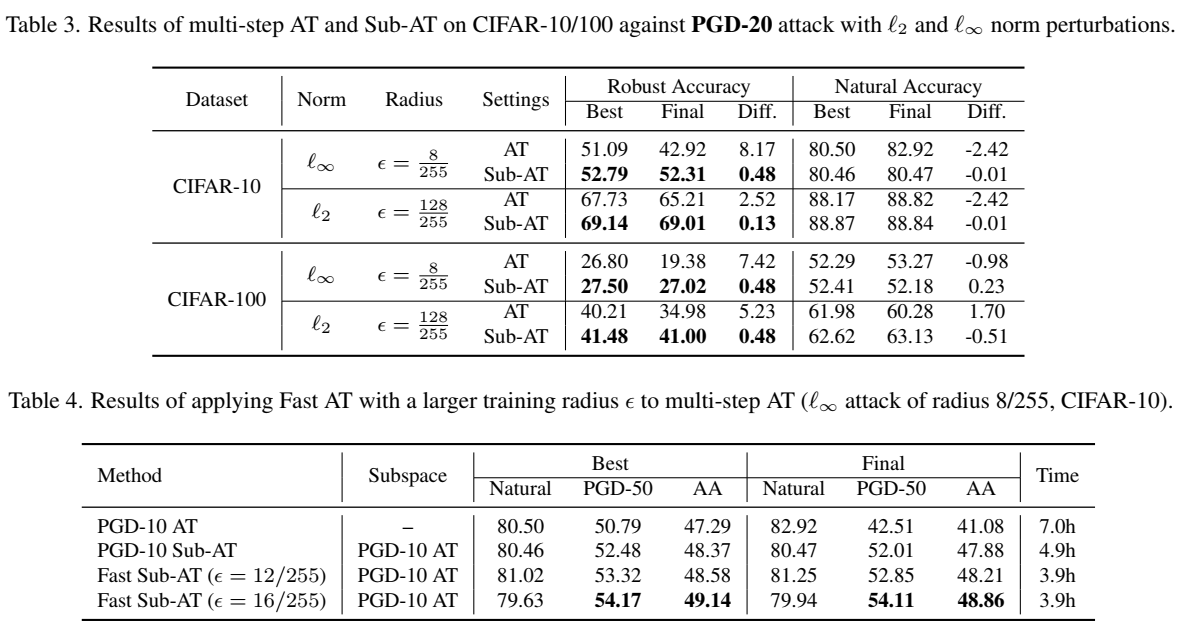
Conclusion

为了控制 AT 中梯度的增加，提出了 Sub-AT 限制 AT 在一个仔细选择的子空间。该方法成功解决了过拟合的问题并显著提高了鲁棒性。

References

如果对你有帮助的话，请给我点个赞吧~

欢迎前往 我的博客 查看更多笔记
  1. 1.Eric Wong, Leslie Rice, and J. Zico Kolter. Fast is better than free: Revisiting adversarial training. In International Conference on Learning Representations (ICLR), 2020. ↩︎
  2. 2.Leslie N Smith. Cyclical learning rates for training neural networks. In 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), pages 464–472. IEEE, 2017. ↩︎
  3. 3.Maksym Andriushchenko and Nicolas Flammarion. Understanding and improving fast adversarial training. In Proceedings of the Advances In Neural Information Processing Systems 33 (NeurIPS), volume 33, pages 16048–16059, 2020. ↩︎
  4. 4.Hoki Kim, Woojin Lee, and Jaewook Lee. Understanding catastrophic overfitting in single-step adversarial training. In AAAI, pages 8119–8127, 2020. ↩︎
  5. 5.Tao Li, Lei Tan, Qinghua Tao, Yipeng Liu, and Xiaolin Huang. Low dimensional landscape hypothesis is true: DNNs can be trained in tiny subspaces. arXiv preprint arXiv:2103.11154, 2021. ↩︎
  6. 6.Leslie Rice, Eric Wong, and Zico Kolter. Overfitting in adversarially robust deep learning. In International Conference on Machine Learning (ICML), pages 8093–8104. PMLR, 2020. ↩︎
  7. 7.Chunyuan Li, Heerad Farkhoor, Rosanne Liu, and Jason Yosinski. Measuring the intrinsic dimension of objective landscapes. In International Conference on Learning Representations (ICLR), 2018. ↩︎
  8. 8.Tao Li, Lei Tan, Qinghua Tao, Yipeng Liu, and Xiaolin Huang. Low dimensional landscape hypothesis is true: DNNs can be trained in tiny subspaces. arXiv preprint arXiv:2103.11154, 2021. ↩︎
--- ♥ end ♥ ---

欢迎关注我呀~