『论文笔记』Gradient Normalization for Generative Adversarial Networks

Information

• Title: Gradient Normalization for Generative Adversarial Networks
• Author: Yi-Lun Wu, Hong-Han Shuai, Zhi Rui Tam, Hong-Yu Chiu
• Institution: (台湾)國立交通大學
• Year: 2021
• Journal: ICCV2021
• Source: arxiv, open access, pdf, Official Code
• Idea: 提出了GN对整个模型进行Lipschitz约束来提高GAN训练的稳定性
• Cite: Yi-Lun Wu, Hong-Han Shuai, Zhi-Rui Tam, Hong-Yu Chiu; Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV), 2021, pp. 6373-6382

@InProceedings{GNGAN_2021_ICCV,
    author = {Yi-Lun Wu, Hong-Han Shuai, Zhi Rui Tam, Hong-Yu Chiu},
    title = {Gradient Normalization for Generative Adversarial Networks},
    booktitle = {Proceedings of the IEEE/CVF International Conference on Computer Vision (ICCV)},
    month = {October},
    year = {2021},
    pages = {6373-6382}
}

Abstract

文章提出了一种通用的 Gradient Normalization(GN) 的方法来解决生成对抗网络(GANs)中由尖锐梯度空间导致的训练不稳定的问题。GN 仅在鉴别器上增加了对梯度范数约束来提高鉴别器的性能。

Introduction

GAN 的评价指标: FID 和 IS 参考: https://blog.csdn.net/qq_35586657/article/details/98478508

GAN 包含两个网络：生成器（目标是生成可以骗过鉴别器的图片），鉴别器（目标是鉴别出生成器生成的图片）。GANs 的一个挑战性的问题是训练过程不稳定，其中一个原因是鉴别器的尖锐梯度空间(sharp gradient space)导致生成器模型崩塌。简单的处理方法是 L2 规范化和权重裁剪，但这种处理方法会导致鉴别器的性能下降。另一种方法是对鉴别器通过正则化和规范化约束Lipschitz连续函数小于一个固定的Lipschitz常数 K, 可以在不牺牲鉴别器性能的条件下平滑梯度空间。

作者认为可以从三个角度考察Lipschitz约束：

• 约束模块还是模型，约束模型的好些，因为约束模块会降低单个模块性能
• 基于采样的还是非基于采样的，如果方法需要从固定的分布进行采样，那就是基于采样的，非采样的好些，基于采样的可能遇到“新样本”时不那么有效
• 严约束还是松约束，定义是梯度范数是否小于一个有限的固定值，严约束更好因为可以避免未见过的样本导致梯度不稳定

目前还没有同时满足约束模块，非采样，严约束的方法，但作者提出的方法 GN 就同时满足，并且很容易迁移到不同类型的网络结构中。

这篇文章的三点贡献：

• 针对 GAN 提出了 GN 很好的平衡了训练过程的稳定性和生成器的性能
• 从理论上证明了 GN 是梯度范数有界的，该性质可以避免生成器遇到梯度爆炸梯度消失的问题并且稳定训练过程
• IS 和 FID 评价的实验结果 SOTA

相关工作

主要提到有两类：正则化(regularization), 规范化(Normalization)

• 正则化：主要是对尖锐梯度进行约束，有基于梯度惩罚的方法，Lipschitz 正则化、一致性约束、正交约束等
• 规范化：例如基于谱范数的规范化、基于权重范数的规范化等。注意到规范化都是非采样的，在训练稳定性上会比正则化更优

$$ D_{KL}(p||q) = \sum_{i=1}^{N} p(x_i)\cdot log\frac{p(x_i)}{q(x_i)} $$

对于 Wasserstein loss 和 WGAN 讲解比较清晰的一篇文章: https://zhuanlan.zhihu.com/p/25071913

及其后续有提到权重裁剪和梯度惩罚：https://www.zhihu.com/question/52602529/answer/158727900

Lipschitz 约束在 GAN 中的作用

对于输入为x的判别器网络可以表示为：

f(x, θ) = W^L + 1a_L(W^L(a_L − 1(W^L − 1(⋯a₁(W¹x)⋯))))

其中，θ := {W¹, ⋯, W^L, W^L + 1}是学习参数集，也就是网络的权重，a_l是非线性激活函数，上述表达式没有考虑偏差。 完整的判别器网络可以表示为：

D(x, θ) = 𝒜(f(x, θ)) 对于GAN而言，判别器的目的是为了区分开真假样本，要最大化目标函数max_DV(G, D)，在固定生成器后得到的判别器最优解为：

$$ D_G^*(x) = \frac{q_{data}(x)}{q_{data}(x) + p_G(x)} = sigmoid(f^*(x)) $$ 我们知道sigmoid的表达式为$\frac{1}{1+e^{-x}}$代入上式可以解出：

f^*(x) = logq_data(x) − logp_G(x) 我们对f^*(x)对x求导：

$$ \nabla_x f^*(x) = \frac{1}{q_{data}(x)} \nabla_x q_{data}(x) - \frac{1}{p_G(x)} \nabla_x p_G(x) $$ 这个导数可以是无限的，甚至是无法计算的，这就会造成判别器失控（一路无限制优化），导致函数空间很大，这就使得D的能力过强，GAN的平衡倾斜。 为了给予判别器于一定限制，这就要Lipschitz假设，通过添加在输入示例x上定义的正则化项来控制鉴别器的Lipschitz常数，此时优化就为：

argmax_{‖f‖Lip ≤ K}V(G, D)

自此，我们看到Lipschitz假设对于GAN的重要性，为了较好实现Lipschitz假设，谱归一化将展示强大的能力。

Method

GAN

基本的GAN网络包含生成器和判别器，数学表述为

生成器 G : ℝ^d_z → ℝⁿ, 判别器 D : ℝⁿ → ℝ, 最小最大化目标是 $$ \begin{aligned} \min_G\max_D\text{ }&\mathbb{E}_{x\sim p_r(x)}\big[log(D(x))\big]+\mathbb{E}_{\tilde{x}\sim p_g(x)}\big[log(1-D(\tilde{x}))\big] \end{aligned} $$ 其中 p_r(x) 表示真实数据分布， p_g(x) 表示由 p_g = G_*(p_z) 定义的分布（* 表示前推测度 ， p_z 是 d_z 维的先验分布）。

前推测度(pushforward measure) 参考 https://en.wikipedia.org/wiki/Pushforward_measure, 大概理解下就是……我不理解 😳

但这里的意思就是 p_g(x) 表示生成样本，整体的思路就是判别器要尽可能把真实样本分为正例，生成样本分为负例，𝔼 表示期望，而生成器的目标相反，尽量使分类器无法区分真实样本和生成样本

GAN很难训练，问题包括但不仅限于梯度消失和梯度爆炸，主要产生的原因是：

1. 优化的目标函数等级与最小化 p_g(x) 和 p_r(x) 的 JS 散度，而当 p_g(x) 和 p_r(x) 没有交集的时候 JS 散度是一个常数，梯度为 0
2. 有限的样本容易是判别器过拟合间接导致梯度爆炸

WGAN 提出了一种新的损失函数 min_Gmax_{D, LD ≤ 1} 𝔼_{x ∼ pr(x)}[D(x)] − 𝔼_{x̃ ∼ pg(x)}[D(x̃)], L_D := inf {L ∈ ℝ : |D(x) − D(y)| ≤ L‖x − y‖, ∀x, y ∈ ℝⁿ} 表示判别器的 Lipschitz 常数，等价于 |D(x) − D(y)| ≤ L_D‖x − y‖, ∀x, y ∈ ℝⁿ. (具体可以看前面提到的那篇文章，讲得很详细)

不过，限制神经网络的Lipschitz常数和提高神经网络的性能之间很难达到一个平衡，有些方法直接对每层的Lipschitz常数进行限制，导致网络的函数空间受到了限制影响性能，而权重裁剪和正则化的方法虽然可以在一个更大的空间内进行搜索，但限制却很弱。

接下来，作者证明了逐层Lipschitz限制网络的Lipschitz常数的上界由其第一个 k 层子网络的任意一层决定。

证明和推导

定义1 用 f_K : ℝⁿ → ℝ 表示一个 K 层网络，该网络可以描述为一系列的仿射变换的嵌套 $$ \begin{aligned} f_K(x)&=\phi_K(\mathbf{W}_K\cdot(\phi_{K-1}(\cdots \mathbf{W}_1\cdot x+\mathbf{b}_1))+\mathbf{b}_K)\\ &=\phi_K(\mathbf{W}_K\cdot f_{K-1}(x)+\mathbf{b}_K), \end{aligned} $$ 其中 W_K ∈ ℝ^{d_K × d_K − 1} 和 b_K ∈ ℝ^d_K 是第 K 层的网络参数, d_K 是目标维度， ϕ_K 是第 K 层的非线性激活函数，用 f_k, ∀k ∈ {1⋯K} 表示第一个 K 层子网。

定义2 用 f_K : ℝⁿ → ℝ 表示一个 K 层网络，令 ∃L_k ≤ L, ∀k ∈ {1⋯K} 则 f_K 表示一个表示一个逐层 L-Lipschitz 现在的网络，L_K 是第 K 层的 Lipschitz 常数： ‖W_k ⋅ x − W_k ⋅ y‖ ≤ L_k‖x − y‖, ∀x, y ∈ ℝ^{d_k − 1}. 引理3 f : ℝⁿ → ℝ 是连续可微函数，L_f 是 f 的 Lipschitz 常数，则 Lipschitz 限制 |f(x) − f(y)| ≤ L_f‖x − y‖, ∀x, y ∈ ℝⁿ 等价于 ‖∇_xf(x)‖ ≤ L_f, ∀x ∈ ℝⁿ

引理3 的证明：

先证充分性：

由 Lipschitz 限制的定义可知 |f(x) − f(y)| ≤ L_f‖x − y‖ 我们考虑 x 在 (y − x) 方向的方向导数的范数 $$ \langle\nabla f(x),\frac{y-x}{\Vert y-x\Vert}\rangle=\lim_{y\rightarrow x}\frac{\vert f(y)-f(x)\vert}{\Vert x-y\Vert}\le L_{f} $$ 其中 ⟨⋅, ⋅⟩ 表示内积，因此梯度的范数是最大的方向导数范数，因此 ‖∇f(x)‖ ≤ L_f 充分性得证，下面证必要性：

根据假设，f 是连续可微的，满足梯度定理条件，因此可以只考虑 y 到 x 的直线的线积分 $$ \begin{align} &\vert f(x)-f(y)\vert\\ &=\Big\vert\int_y^x\nabla f(r) dr\Big\vert\\ &=\Big\vert\int_0^1\langle \nabla f(xt+y(1-t)),x-y\rangle dt\Big\vert\\ &\le\Big\vert\int_0^1\Vert \nabla f(xt+y(1-t))\Vert\cdot\Vert x-y\Vert dt\Big\vert\\ &\le L_{f} \Big\vert\int_0^1\Vert x-y\Vert dt\Big\vert\\ &=L_{f}\Vert x-y\Vert. \end{align} $$ 因此必要性得证。

引理 3 启发作者设计一种直接约束梯度范数的规范化方法。

假设4 f : ℝⁿ → ℝ 表示由神经网络定义的连续函数，且 f 的所有激活函数都是分段线性的，因此 f 也是近乎可微的。

定理5 f_K : ℝⁿ → ℝ 表示一个逐层 1-Lipschitz 约束的 K 层网络，第一个 k 层网络的 Lipschitz 常数上限 L_fk 由 L_fk − 1 决定，即： L_fk ≤ L_fk − 1, ∀k ∈ {2⋯K}

证明：

因为所有层都包含了激活函数且都是 1-Lipschitz 约束，那么 $$ \begin{aligned} \Vert \mathbf{W}_k\cdot x-\mathbf{W}_k\cdot y\Vert&\le\Vert x-y\Vert,\forall x,y\in\mathbb{R}^{d_{k-1}}\\ L_{\phi_k}&=1. \end{aligned} $$ 由上式我们可以推出第 k 层的特征距离上限： $$ \begin{aligned} &\Vert f_k(x)-f_k(y) \Vert \\ &=\Vert\phi_k(\mathbf{W}_k\cdot f_{k-1}(x)+\mathbf{b}_k)-\phi_k(\mathbf{W}_k\cdot f_{k-1}(y)+\mathbf{b}_k)\Vert \\ &\le L_{\phi_k}\Vert(\mathbf{W}_k\cdot f_{k-1}(x)+\mathbf{b}_k)-(\mathbf{W}_k\cdot f_{k-1}(y)+\mathbf{b}_k)\Vert \\ &\le L_{\phi_k}L_k\Vert f_{k-1}(x)-f_{k-1}(y)\Vert \\ &= \Vert f_{k-1}(x)-f_{k-1}(y)\Vert. \\ \end{aligned} $$ 即 $$ \frac{\Vert f_k(x)-f_k(y)\Vert}{\Vert x-y\Vert}\le\frac{\Vert f_{k-1}(x)-f_{k-1}(y)\Vert}{\Vert x-y\Vert}, \forall x,y \in\mathbb{R}^n $$ 证毕

定理5当且仅当 ∃x, y ∈ ℝⁿ 且满足下式时成立 $$ \frac{\Vert f_k(x)-f_k(y)\Vert}{\Vert x-y\Vert}=\frac{\Vert f_{k-1}(x)-f_{k-1}(y)\Vert}{\Vert x-y\Vert}=L_{f_{k-1}} $$ 否则 L_fk < L_fk − 1 < ⋯ < L_f1 ≤ 1 即 Lipschitz 常数逐层减小，另一方面，也不必逐层Lipschitz约束，而是可以构建整个Lipschitz模型。根据引理 3，作者提出了 Gradient Normalization (GN).

GN 对梯度范数 ‖∇_xf(x)‖ 进行规范化且同时限制了 f(x) : $$ \hat{f}(x)=\frac{f(x)}{\Vert\nabla_x f(x)\Vert+\zeta(x)} $$ 其中 ζ(x) : ℝⁿ → ℝ 是一个通用项，可以是常数或者与 f(x) 相关避免 |f̂(x)| 变成无穷大或 ‖∇_xf̂(x)‖ 近乎0. 作者将 ζ(x) 设置为 |f(x)| 并证明 GN 是满足 1-Lipschitz 约束

定理6 将 f : ℝⁿ → ℝ 定义为有神经网络建模的连续函数，并且网络中的所有激活函数都是分段线性的。规范化函数 f̂(x) = f(x)/(‖∇_xf(x)‖+|f(x)|) 是梯度范数的界限，因为 $$ \Vert\nabla_x\hat{f}(x)\Vert=\Bigg\vert\frac{\Vert\nabla f\Vert}{\Vert\nabla f\Vert+\vert f\vert}\Bigg\vert^2\le 1 $$

证明：

简单起见，这里忽略函数参数。由 f̂(x) 的梯度范数定义得： $$ \begin{align} \Vert\nabla\hat{f}\Vert &=\Bigg\Vert\nabla\bigg(\frac{f}{\Vert\nabla f\Vert+\vert f\vert}\bigg)\Bigg\Vert \\ &=\Bigg\Vert\frac{\nabla f\big(\Vert\nabla f\Vert+\vert f\vert\big)-f\nabla\big(\Vert\nabla f\Vert+\vert f\vert\big)}{\big(\Vert\nabla f\Vert+\vert f\vert\big)^2}\Bigg\Vert. \label{th5:pfeq2} \end{align} $$ 由链式规则，可以推出 $$ \begin{align} \nabla\Vert\nabla f\Vert&=\nabla^2 f\frac{\nabla f}{\Vert\nabla f\Vert}, \\ \nabla\vert f\vert&=\nabla f\frac{f}{\vert f\vert}. \end{align} $$ 由于神经网络中的激活函数都是分段线性的，所以其 Hessian 矩阵 ∇²f 是 0 矩阵，前面的式子可以化简为 $$ \begin{aligned} \Vert\nabla\hat{f}\Vert =\Bigg\Vert\frac{\Vert\nabla f\Vert^2}{\big(\Vert\nabla f\Vert+\vert f\vert\big)^2}\Bigg\Vert =\Bigg\Vert\frac{\Vert\nabla f\Vert}{\Vert\nabla f\Vert+\vert f\vert}\Bigg\Vert^2\le 1. \end{aligned} $$ 即定理 6

考虑到如果鉴别器过拟合可能会出现 f(x) → ±∞ 和 ‖∇_xf(x)‖ → 0 的情况，以及 ζ(x) = 0 和 ζ(x) = 1 两种常见情况。

image-20220727211521407

因为函数范数 |f(x)| 不直接与梯度范数相关，所以对于极端预测结果可能是规范化的梯度范数‖∇_xf̂(x)‖ 和规范化的函数值 |f̂(x)| 爆炸，所以提出将 ζ(x) 设置为 |f(x)| 。这种自动调整的机制能防止生成器获得爆炸梯度，以此可以稳定GAN的训练过程。伪代码如下：

image-20220727214021252

GN的梯度分析: f̂(x) 对 W_k 的的梯度如下： $$ $$ 从最后一个等式可以看出，GN 是自适应梯度正则化的特殊形式。而第一个等式中，第一项是GAN的目标梯度，用于提高鉴别器的性能，而第二项是正则项，用自适应的正则化参数惩罚 f 的梯度范数。这种梯度惩罚更灵活，因此这种自平衡机制强迫GN达到严 Lipschitz 约束。

---

Experiment

• 数据集：
  • CIFAR10: 包含 60K 大小为 32 × 32 × 3 的图像，划分为 50K 训练集和 10K 测试集
  • STL-10：无监督数据集，48 × 48 × 3, 包含 5k 训练数据，8k 测试数据和 100k 无标签数据
  • CelebA-HQ: 超分辨率数据集, 30k 大小为 256 × 256 × 3 人脸图像
  • LSUN Church Outdoor：超分辨率数据集, 包含 126k 大小为 256 × 256 × 3 的教堂户外景象
• 验证标准：Inception Score (IS)和 Frechet Inception Distance (FID)
• 损失函数：因为 GN 的输出为 [−1, 1] 会使 Wasserstein loss 退化为 hinge loss
  • hinge loss
  • nonsaturating loss (NS)

无条件图像生成

image-20220728140615776

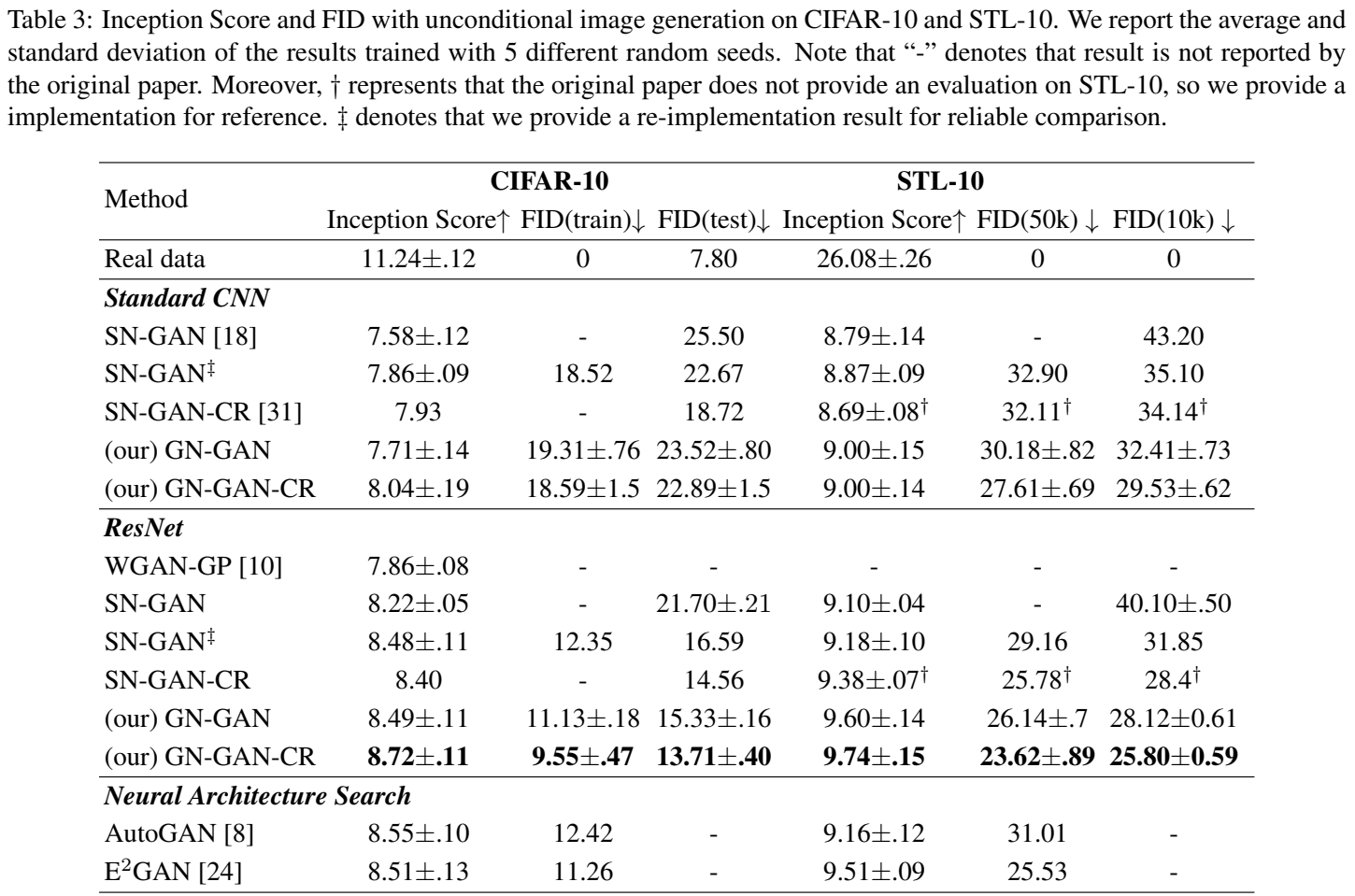
GN-GAN 联合 consistency regularization (CR) 标记为 GN-GAN-CR

有条件图像生成

image-20220728143929101

无条件大尺寸图片生成

image-20220728144240350

附加材料有更多的图片展示

定理5的实验分析

image-20220728145414554

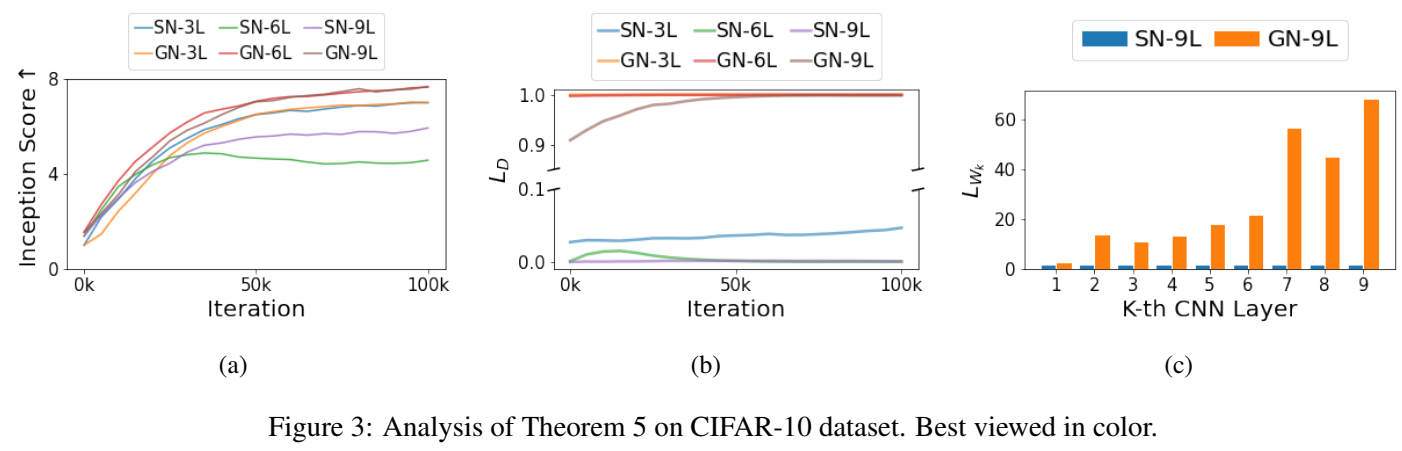
根据定理5，随着层数增加，Lipschitz常数减小。上图展示了对 SN 和 GN 使用 wasserstein loss 的测试，nL 表示生成器和鉴别器的卷积层的数量，可见SN的鉴别器Lipschitz常数远小于1. 此外，SN-GAN 的所有鉴别器在Lipschitz约束L_D ≤ 1下都不能很好地近似的 Wasserstein 距离，即使上述推论保证了最优鉴别器的存在，作者认为这是因为SN过度约束了鉴别器的Lipschitz常数以至于鉴别器无法提高Lipschitz常数并接近理论最优。

消融实验

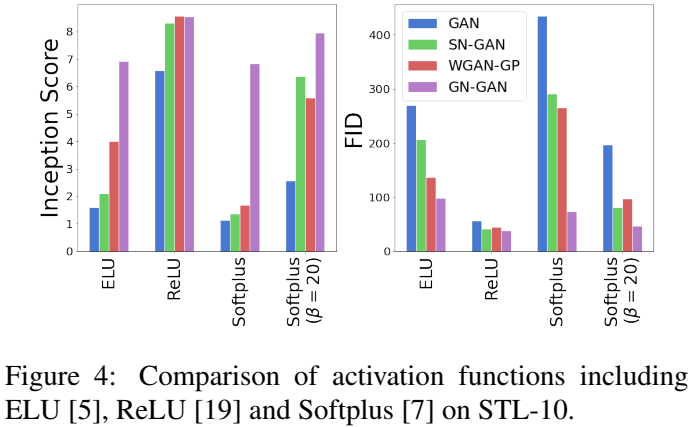
激活函数 定理6的前提是激活函数是分段线性的，作者测试了不同激活函数下的效果对比

image-20220728152419262

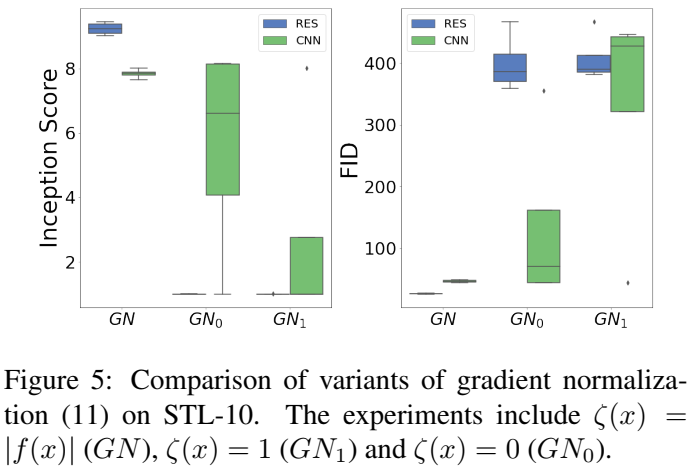
GN变量 如图所示

image-20220728152534286

---

Conclusion

提出了一种简单实现的梯度规范化方法GN用于稳定GANs的训练，并证明了其满足严Lipschitz约束并使任意鉴别器作为Lipschitz连续函数。实验中在不同结构的网络和不同数据集中取得了SOTA结果。

作者计划后续用类似的方法替换GN的分母来减少计算量，还有就是在一些其他生成任务。

Code Analysis

开源代码仓库中提到 GN 任意迁移到其他 GAN 网络结构中，

from torch.nn import BCEWithLogitsLoss
from models.gradnorm import normalize_gradient

net_D = ...     # discriminator
net_G = ...     # generator
loss_fn = BCEWithLogitsLoss()

# Update discriminator
x_real = ...                                    # real data
x_fake = net_G(torch.randn(64, 3, 32, 32))      # fake data
pred_real = normalize_gradient(net_D, x_real)   # net_D(x_real)
pred_fake = normalize_gradient(net_D, x_fake)   # net_D(x_fake)
loss_real = loss_fn(pred_real, torch.ones_like(pred_real))
loss_fake = loss_fn(pred_fake, torch.zeros_like(pred_fake))
(loss_real + loss_fake).backward()              # backward propagation
...

# Update generator
x_fake = net_G(torch.randn(64, 3, 32, 32))      # fake data
pred_fake = normalize_gradient(net_D, x_fake)   # net_D(x_fake)
loss_fake = loss_fn(pred_fake, torch.ones_like(pred_fake))
loss.backward()                                 # backward propagation
...

关键代码在第 20 行 pred_fake = normalize_gradient(net_D, x_fake) # net_D(x_fake)，我们进入函数内部查看，函数实现仅8行

def normalize_gradient(net_D, x, **kwargs):
    """
                     f
    f_hat = --------------------
            || grad_f || + | f |
    """
    x.requires_grad_(True)
    f = net_D(x, **kwargs)
    grad = torch.autograd.grad(
        f, [x], torch.ones_like(f), create_graph=True, retain_graph=True)[0]
    grad_norm = torch.norm(torch.flatten(grad, start_dim=1), p=2, dim=1)
    grad_norm = grad_norm.view(-1, *[1 for _ in range(len(f.shape) - 1)])
    f_hat = (f / (grad_norm + torch.abs(f)))
    return f_hat

从前面的代码中我们可以了解到，函数声明中的两个参数 net_D 和 x 分别是鉴别器网络和生成器生成的图片，下面逐行分析代码

1. 第 7, 8 行: 将 x 的梯度计算打开，然后传入鉴别器中进行前向传播
2. 第 9, 10 行: 计算鉴别器输出对输入图像的导数
3. 第 11 行：将梯度值展平为二维并计算范数，实际上展平操作有些多余了，和 torch.norm(grad, p=2, dim=(1, 2, 3)) 是等价的
4. 第 12 行：调整梯度范数
5. 第 13 行：GN操作

在解读代码之前，我以为GN是针对网络权重进行规范化的，在看完代码后，GN实质上还是对特征进行规范化，但GN没有改动特征图，而是只对网络的输出进行规范化来达到限制网络的Lipschitz常数的作用，这是一个值得借鉴的思路

GAN

训练

借此机会分析一下 GAN 的训练过程，给代码加了详细的注释，据此对 GAN 网络的训练有了更深的了解

def train():
    # 获取数据，最后的 looper 是一个可以无限循环的从 dataloader 中取数据的迭代器
    dataset = get_dataset("cifar10.32")
    dataloader = torch.utils.data.DataLoader(
        dataset=dataset,
        batch_size=64 * 5,
        shuffle=True,
        num_workers=8,
        drop_last=True)
    looper = infiniteloop(dataloader)

    # model, 创建模型
    net_G = net_G_models["resnet.32"](128, 1).cuda()
    ema_G = net_G_models["resnet.32"](128, 1).cuda()
    net_D = net_D_models["resnet.32"](1).cuda()

    # ema, 权重衰减，将 源模型 按照 衰减比例 迁移到目标模型
    # 但这里衰减为 0 是将 源模型 完全复制到 目标模型
    # ema(source, target, decay)
    ema(net_G, ema_G, decay=0)

    # loss: HingeLoss()
    loss_fn = loss_fns["hinge"]()

    # optimizer, 常规优化器
    optim_G = optim.Adam(net_G.parameters(), lr=0.0002, betas=[0.0, 0.9])
    optim_D = optim.Adam(net_D.parameters(), lr=0.0004, betas=[0.0, 0.9])

    # scheduler, 其实就是一个线性下降的学习率控制方法
    def decay_rate(step):
        period = max(200000 - 0, 1)
        return 1 - max(step - 0, 0) / period
    sched_G = optim.lr_scheduler.LambdaLR(optim_G, lr_lambda=decay_rate)
    sched_D = optim.lr_scheduler.LambdaLR(optim_D, lr_lambda=decay_rate)

    # 统计一下两个网络的参数量(其实完全可以用个 sum 一行完成)
    D_size = 0
    for param in net_D.parameters():
        D_size += param.data.nelement()
    G_size = 0
    for param in net_G.parameters():
        G_size += param.data.nelement()
    print('D params: %d, G params: %d' % (D_size, G_size))

    # tensorboard 的记录器
    writer = SummaryWriter("./logs/GN-GAN_CIFAR10_RES_0")
    # 加载断点(checkpoint)
    if FLAGS.resume:
        ckpt = torch.load(os.path.join("./logs/GN-GAN_CIFAR10_RES_0", 'model.pt'))
        net_G.load_state_dict(ckpt['net_G'])
        net_D.load_state_dict(ckpt['net_D'])
        ema_G.load_state_dict(ckpt['ema_G'])
        optim_G.load_state_dict(ckpt['optim_G'])
        optim_D.load_state_dict(ckpt['optim_D'])
        sched_G.load_state_dict(ckpt['sched_G'])
        sched_D.load_state_dict(ckpt['sched_D'])
        fixed_z = ckpt['fixed_z']
        fixed_y = ckpt['fixed_y']
        # start value
        start = ckpt['step'] + 1
        best_IS, best_FID = ckpt['best_IS'], ckpt['best_FID']
        del ckpt
    else:
        # sample fixed z 用于生成图片的随机数，每轮都输入到生成网络中，用于观察生成网络的生成图像变化
        fixed_z = torch.randn(64, 128).cuda()
        fixed_y = torch.randint(1, (64,)).cuda()
        # start value
        start, best_IS, best_FID = 1, 0, 999

        os.makedirs(os.path.join("./logs/GN-GAN_CIFAR10_RES_0", 'sample'))
        # 将配置文件记录下来
        with open(os.path.join("./logs/GN-GAN_CIFAR10_RES_0", "flagfile.txt"), 'w') as f:
            f.write(FLAGS.flags_into_string())
        # 将一些数据集的图片上传到 tensorboard
        real = next(iter(dataloader))[0][:64]
        writer.add_image('real_sample', make_grid((real + 1) / 2))
        writer.flush()

    # tqdm 一个显示进度条的小工具
    with trange(start, 200000 + 1, ncols=0,
                initial=start - 1, total=200000) as pbar:
        # 开始训练
        for step in pbar:
            loss_sum = 0
            loss_real_sum = 0
            loss_fake_sum = 0
            loss_cr_sum = 0

            # 读取数据，按照默认配置，读取的数据可以划分为 5 个 64 的 batch
            x, y = next(looper)
            x = iter(torch.split(x, 64))
            y = iter(torch.split(y, 64))
            # Discriminator 先训练鉴别器
            for _ in range(5):
                optim_D.zero_grad()
                # 获取数据集的真实数据
                x_real, y_real = next(x).cuda(), next(y).cuda()

                # 使用生成器生成一些假图和假标签
                with torch.no_grad():
                    z_ = torch.randn(64, 128).cuda()
                    y_fake = torch.randint(1, (64,)).cuda()
                    x_fake = net_G(z_, y_fake).detach()
                # 将真图和假图拼在一起组成一个 batch
                x_real_fake = torch.cat([x_real, x_fake], dim=0)
                y_real_fake = torch.cat([y_real, y_fake], dim=0)
                # 使用论文提出的 Norm 方法进行前向传播
                pred = normalize_gradient(net_D, x_real_fake, y=y_real_fake)
                # 将输出结果划分，真图和假图的输出结果分开
                pred_real, pred_fake = torch.split(pred, [x_real.shape[0], x_fake.shape[0]])

                # 将真假图的输出传入损失函数计算返回总损失、真图损失和假图损失
                loss, loss_real, loss_fake = loss_fn(pred_real, pred_fake)
                # consistency_loss 是对做了数据增强后的网络输出计算loss
                if FLAGS.cr > 0:  # 默认值 FLAGS.cr = 0
                    loss_cr = consistency_loss(net_D, x_real, y_real, pred_real)
                else:
                    loss_cr = torch.tensor(0.)
                loss_all = loss + FLAGS.cr * loss_cr
                # 反向传播并更新网络
                loss_all.backward()
                optim_D.step()

                # 统计 loss
                loss_sum += loss.cpu().item()
                loss_real_sum += loss_real.cpu().item()
                loss_fake_sum += loss_fake.cpu().item()
                loss_cr_sum += loss_cr.cpu().item()

            # 计算该轮训练中每个 batch 的 loss
            loss = loss_sum / 5
            loss_real = loss_real_sum / 5
            loss_fake = loss_fake_sum / 5
            loss_cr = loss_cr_sum / 5

            # 将 loss 发布到 tensorboard 上
            writer.add_scalar('loss', loss, step)
            writer.add_scalar('loss_real', loss_real, step)
            writer.add_scalar('loss_fake', loss_fake, step)
            writer.add_scalar('loss_cr', loss_cr, step)

            pbar.set_postfix(
                loss_real='%.3f' % loss_real,
                loss_fake='%.3f' % loss_fake)

            # Generator 接下来训练生成器
            # 先将鉴别器的梯度缓存下来，并关掉梯度记录，训练完后再打开梯度记录并恢复缓存
            with module_no_grad(net_D):
                # 常规的深度网络训练，输入数据是随机产生的随机向量
                optim_G.zero_grad()
                z_ = torch.randn(128, 128).cuda()
                y_ = torch.randint(1, (128,)).cuda()
                fake = net_G(z_, y_)
                pred_fake = normalize_gradient(net_D, fake, y=y_)
                loss = loss_fn(pred_fake)
                loss.backward()
                optim_G.step()

            # ema 生成器权重衰减
            if step < 0:
                decay = 0
            else:
                decay = 0.999
            ema(net_G, ema_G, decay)

            # scheduler
            sched_G.step()
            sched_D.step()

            # sample from fixed z
            # 用固定的输入输入到生成器中产生假图并保存
            if step == 1 or step % FLAGS.sample_step == 0:
                with torch.no_grad():
                    fake_net = net_G(fixed_z, fixed_y).cpu()
                    fake_ema = ema_G(fixed_z, fixed_y).cpu()
                grid_net = (make_grid(fake_net) + 1) / 2
                grid_ema = (make_grid(fake_ema) + 1) / 2
                writer.add_image('sample_ema', grid_ema, step)
                writer.add_image('sample', grid_net, step)
                save_image(
                    grid_ema,
                    os.path.join("./logs/GN-GAN_CIFAR10_RES_0", 'sample', '%d.png' % step))

            # evaluate IS, FID and save model
            # 验证并记录几个指标
            if step == 1 or step % FLAGS.eval_step == 0:
                (IS, IS_std), FID = evaluate(net_G)
                (IS_ema, IS_std_ema), FID_ema = evaluate(ema_G)
                if not math.isnan(FID) and not math.isnan(best_FID):
                    save_as_best = (FID < best_FID)
                else:
                    save_as_best = (IS > best_IS)
                if save_as_best:
                    best_IS = IS
                    best_FID = FID
                ckpt = {
                    'net_G': net_G.state_dict(),
                    'net_D': net_D.state_dict(),
                    'ema_G': ema_G.state_dict(),
                    'optim_G': optim_G.state_dict(),
                    'optim_D': optim_D.state_dict(),
                    'sched_G': sched_G.state_dict(),
                    'sched_D': sched_D.state_dict(),
                    'fixed_y': fixed_y,
                    'fixed_z': fixed_z,
                    'best_IS': best_IS,
                    'best_FID': best_FID,
                    'step': step,
                }
                if step == 1 or step % FLAGS.save_step == 0:
                    torch.save(
                        ckpt, os.path.join("./logs/GN-GAN_CIFAR10_RES_0", '%06d.pt' % step))
                if save_as_best:
                    torch.save(
                        ckpt, os.path.join("./logs/GN-GAN_CIFAR10_RES_0", 'best_model.pt'))
                torch.save(ckpt, os.path.join("./logs/GN-GAN_CIFAR10_RES_0", 'model.pt'))
                metrics = {
                    'IS': IS,
                    'IS_std': IS_std,
                    'FID': FID,
                    'IS_EMA': IS_ema,
                    'IS_std_EMA': IS_std_ema,
                    'FID_EMA': FID_ema,
                }
                for name, value in metrics.items():
                    writer.add_scalar(name, value, step)
                writer.flush()
                with open(os.path.join("./logs/GN-GAN_CIFAR10_RES_0", 'eval.txt'), 'a') as f:
                    metrics['step'] = step
                    f.write(json.dumps(metrics) + "\n")
                k = len(str(200000))
                pbar.write(
                    f"{step:{k}d}/{200000} "
                    f"IS: {IS:6.3f}({IS_std:.3f}), "
                    f"FID: {FID:.3f}, "
                    f"IS_EMA: {IS_ema:6.3f}({IS_std_ema:.3f}), "
                    f"FID_EMA: {FID_ema:.3f}")
    writer.close()

验证

def generate_images(net_G):
    images = []
    with torch.no_grad():
        # tqdm 的进度条迭代，等价于 range
        for _ in trange(0, FLAGS.num_images, FLAGS.batch_size_G, ncols=0, leave=False):
            # 产生一组随机数输入到生成器中生成假图
            z = torch.randn(FLAGS.batch_size_G, FLAGS.z_dim).to(device)
            y = torch.randint(FLAGS.n_classes, (FLAGS.batch_size_G,)).to(device)
            fake = (net_G(z, y) + 1) / 2
            images.append(fake.cpu())
    # 将假图拼接起来返回
    images = torch.cat(images, dim=0)
    return images[:FLAGS.num_images]

def evaluate(net_G):
    # 生成一组假图
    images = generate_images(net_G=net_G)
    # 使用 pytorch_gan_metrics 库中的函数计算 IS 和 FID
    (IS, IS_std), FID = get_inception_score_and_fid(images, FLAGS.fid_stats, verbose=True)
    del images
    return (IS, IS_std), FID

损失函数

看看一些损失函数的实现

import torch
import torch.nn as nn
import torch.nn.functional as F

class BCEWithLogits(nn.Module):
    def __init__(self):
        super().__init__()
        self.bce = nn.BCEWithLogitsLoss()

    def forward(self, pred_real, pred_fake=None):
        if pred_fake is not None:
            loss_real = self.bce(pred_real, torch.ones_like(pred_real))
            loss_fake = self.bce(pred_fake, torch.zeros_like(pred_fake))
            loss = loss_real + loss_fake
            return loss, loss_real, loss_fake
        else:
            loss = self.bce(pred_real, torch.ones_like(pred_real))
            return loss


class HingeLoss(nn.Module):
    def forward(self, pred_real, pred_fake=None):
        if pred_fake is not None:
            loss_real = F.relu(1 - pred_real).mean()
            loss_fake = F.relu(1 + pred_fake).mean()
            loss = loss_real + loss_fake
            return loss, loss_real, loss_fake
        else:
            loss = -pred_real.mean()
            return loss


class Wasserstein(nn.Module):
    def forward(self, pred_real, pred_fake=None):
        if pred_fake is not None:
            loss_real = pred_real.mean()
            loss_fake = pred_fake.mean()
            loss = -loss_real + loss_fake
            return loss, loss_real, loss_fake
        else:
            loss = -pred_real.mean()
            return loss


class BCE(nn.Module):
    def __init__(self):
        super().__init__()
        self.bce = nn.BCELoss()

    def forward(self, pred_real, pred_fake=None):
        if pred_fake is not None:
            loss_real = self.bce(
                (pred_real + 1) / 2, torch.ones_like(pred_real))
            loss_fake = self.bce(
                (pred_fake + 1) / 2, torch.zeros_like(pred_fake))
            loss = loss_real + loss_fake
            return loss, loss_real, loss_fake
        else:
            loss = self.bce(
                (pred_real + 1) / 2, torch.ones_like(pred_real))
            return loss

References

• 生成对抗网络（GAN）
• SN-GAN论文解读
• 详细解析深度学习中的 Lipschitz 条件
• GAN的几种评价指标
• 令人拍案叫绝的Wasserstein GAN
• 详解 pytorch 中的 autograd.grad() 函数

---

如果对你有帮助的话，请给我点个赞吧~

欢迎前往 我的博客 查看更多笔记