小鲸鱼的梦境
0%

『LeetCode』725 分隔链表

发表于 更新于 分类于 Valine：
本文字数： 3.4k 阅读时长 ≈ 3 分钟

题目

725. 分隔链表

难度: 中等

给定一个头结点为 \(root\) 的链表, 编写一个函数以将链表分隔为 \(k\) 个连续的部分。

每部分的长度应该尽可能的相等: 任意两部分的长度差距不能超过 1，也就是说可能有些部分为 null。

这k个部分应该按照在链表中出现的顺序进行输出，并且排在前面的部分的长度应该大于或等于后面的长度。

返回一个符合上述规则的链表的列表。

举例： 1->2->3->4, k = 5 // 5 结果 [ [1], [2], [3], [4], null ]

示例 1：

输入:
root = [1, 2, 3], k = 5
输出: [[1],[2],[3],[],[]]
解释:
输入输出各部分都应该是链表，而不是数组。
例如, 输入的结点 root 的 val= 1, root.next.val = 2, \\root.next.next.val = 3, 且 root.next.next.next = null。
第一个输出 output[0] 是 output[0].val = 1, output[0].next = null。
最后一个元素 output[4] 为 null, 它代表了最后一个部分为空链表。

示例 2：

输入:
root = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10], k = 3
输出: [[1, 2, 3, 4], [5, 6, 7], [8, 9, 10]]
解释:
输入被分成了几个连续的部分，并且每部分的长度相差不超过1.前面部分的长度大于等于后面部分的长度。

\(\quad\)

提示:

  • \(root\) 的长度范围： \([0, 1000]\).
  • 输入的每个节点的大小范围：[0, 999].
  • \(k\) 的取值范围： \([1, 50]\).

解析及代码示例

方法一 计算长度

简要说说，就是先遍历一次链表计算出链表长度 \(n\) ，然后根据 \(n // k\) 就能计算出分割后每段的长度，其中前 \(n \\% k\) 段长度比其他段长1。

链表基本操作，代码略。

方法二 快慢K指针

快慢双指针是众所周知的查找链表中间结点且只需遍历链表一次的方法，实现原理是快指针每次走 2 步，慢指针每次走 1 步，假设链表长度为 \(n\) ，当快指针走了 \(n\) 步到达链表末尾时，慢指针只走了 \(\frac{1}{2}n\) 步位于链表中间

同理，假设我们需要查找链表的三等分点，那么可以设置三个指针，第一个指针每次走 1 步，第二个指针每次走 2 步，第三个指针每次走 3 步，那么当第三个指针走了 \(n\) 步到达链表末尾时，第一个指针走了 \(\frac{1}{3}n\) 步位于第一个三等分点，第二个指针走了 \(\frac{2}{3}n\) 步位于第二个三等分点。

以此类推，若我们需要将链表分为 K 段，就需要 K 个指针，第一个指针每次走 1 步，第二个指针每次走 2 步，……，第K个指针每次走 K 步，当第 K 个指针到达链表末尾时，其他 K - 1 个指针分别位于 \(\frac{1}{k}, \frac{2}{k}, \dots, \frac{k-1}{k}\) 的位置

下图以链表 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 9, K = 4 为例展示了通过快慢 K 指针的方法将链表分成 K 段

初始位置所有指针都位于dummy结点，但此题保证root非空，就不再设哑结点，初始状态设为依次指向前 K 个结点，此时各段仅有一个结点(虚线框内结点)

第一轮

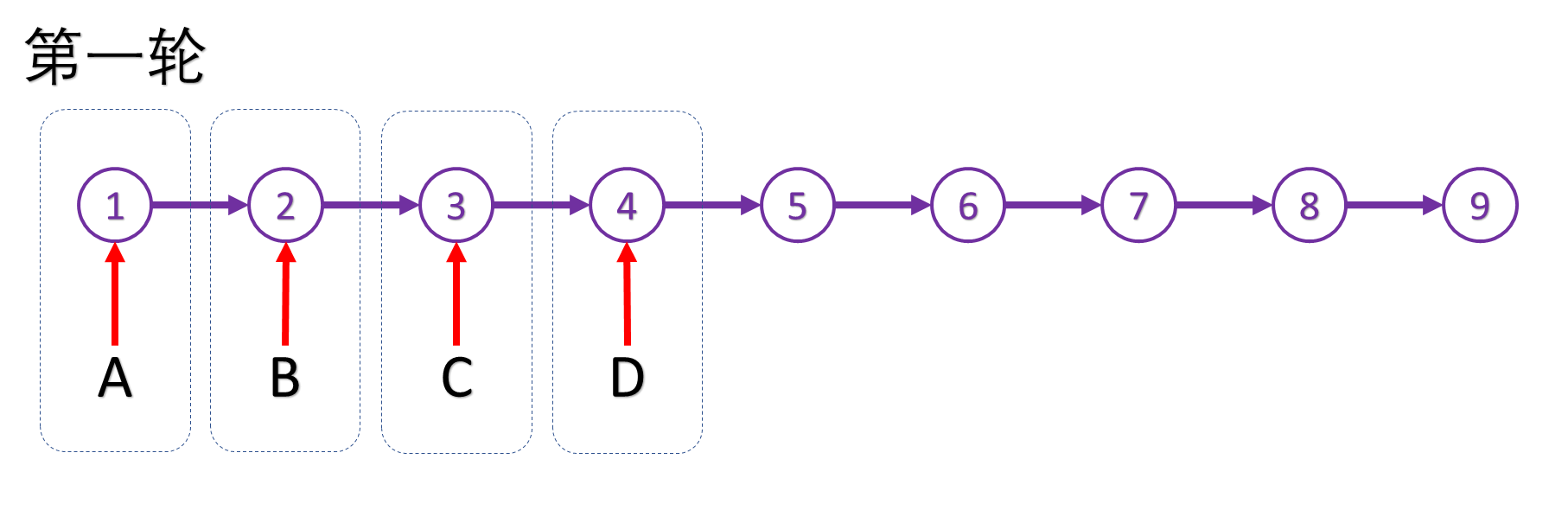
A 指针前进 1 步，B 指针前进 2 步，C 指针前进 3 步，D 指针前进 4 步，此时各段都有两个结点

第二轮

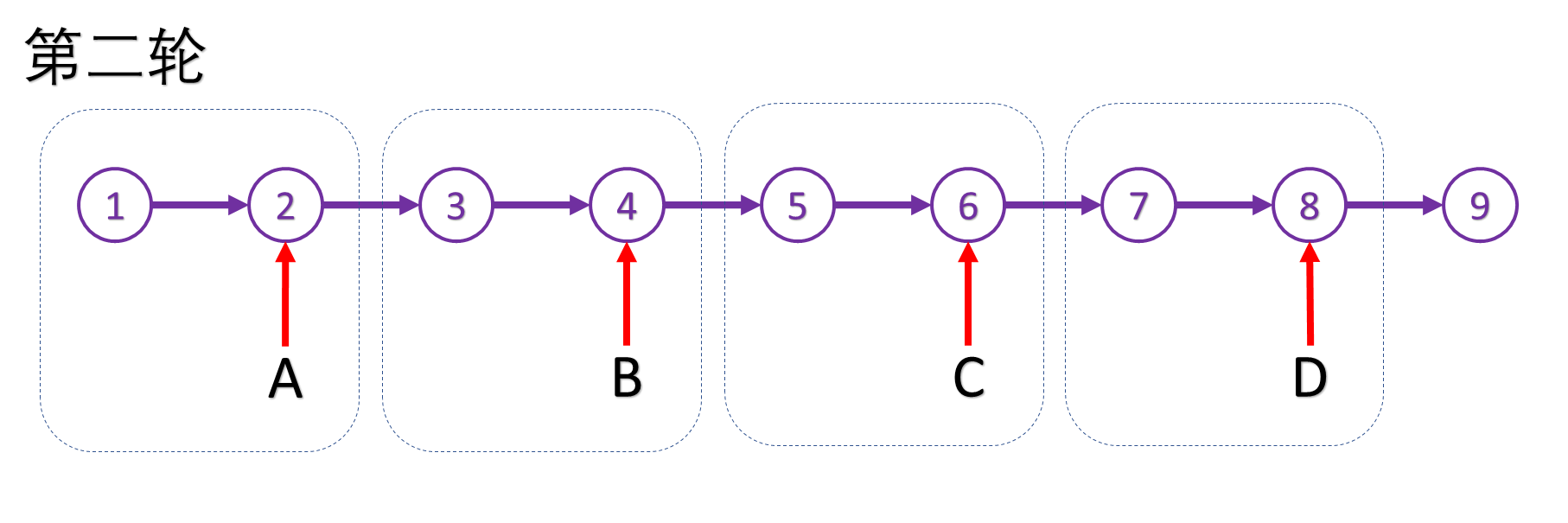
剩下的结点只有 1 个不足 K 个了，只能允许第一段多一个，表现为四个指针都只前进 1 步

第三轮

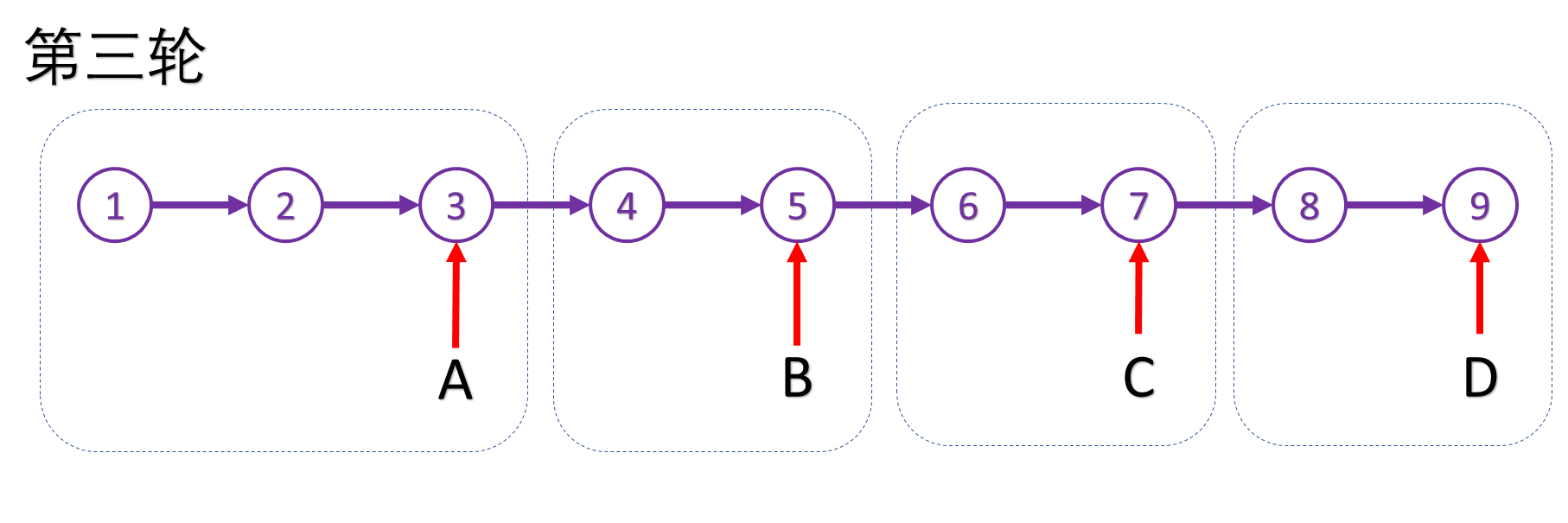
最后，将链表断开，各指针指回各段头结点

结束

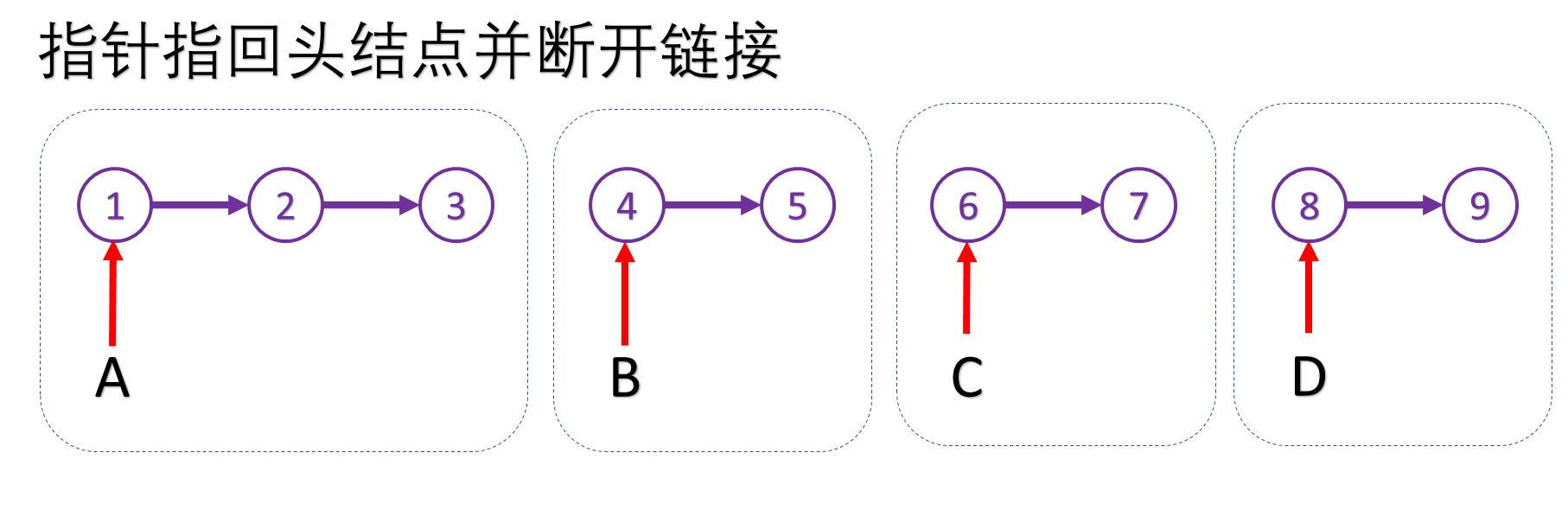
注意事项

  1. 注意链表为空，链表结点数不足 K 个的情况
  2. 关于各指针移动的情况
    • 使用第 K 个指针作为判断结束与否的标志，此指针单独处理
    • 为了保证“前面部分的长度大于等于后面部分的长度”，指针需要这样移动：
      1. 所有指针向后移动一位(等价于第一段增加了一个结点)
      2. 除第一个结点为其他指针向后移动一位(等价于第二段增加了一个结点)
      3. 依次类推，处理前 K-1 个结点
      4. 第 K 个结点需要先与其他结点移动，若第 K 个结点以经到了链表末尾，说明已经没有结点可以分配给前面的段了，链表分段完毕
  3. 移动完后的情况是：第 K 个指针为空，其他指针指向自己段的末尾结点，此时：
    1. 第一段的头结点就是root结点
    2. 第二段的头结点可以由指向第一段末尾结点的指针寻得，以此类推
    3. 此时需要做两件事，一是断开段与段之间的链接，二是将指针移到当前段头结点，聪明的你应该已经知道我要说什么了，移动指针到当前段头结点需要借助上一段的末尾结点指针，所以我们必须先将指针移动到当前段头结点，再将当前段与前一段的链接断开，这个过程是由后往前的

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/* Code language: C/C++ */
class Solution {
public:
    vector<ListNode*> splitListToParts(ListNode* root, int k) {
        vector<ListNode*> ans(k, nullptr);
        ans[0] = root;
        /* 初始化指针数组，按顺序指向前k个结点 */
        for (int i = 1; i < k; ++i)
            if (ans[i - 1] != nullptr)
                ans[i] = ans[i - 1]->next;
        /* 移动指针，数组下标为 i 的指针每次前进 i + 1 */
        while (ans[k - 1] != nullptr) {
            for (int i = 0; i < k - 1; ++i) {
                ans[k - 1] = ans[k - 1]->next;
                if (ans[k - 1] == nullptr) break;
                for (int j = i; j < k - 1; ++j)
                    ans[j] = ans[j]->next;
            }
            if (ans[k - 1] != nullptr) ans[k - 1] = ans[k - 1]->next;
        }
        /* 此时链表已经由 k - 1 个指针划分为 k 段，数组中的指针均指向各段最后一个结点 */
        /* 将链表分割成 k 段，并将数组指针设为各段的头结点, 即上一段最后一个结点的next指针指向的结点 */
        for (int i = k - 1; i > 0; --i)
            if (ans[i - 1] != nullptr) {
                ans[i] = ans[i - 1]->next;
                ans[i - 1]->next = nullptr;
            }
        /* 第一段的头结点为 root */
        ans[0] = root;
        return ans;
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Code language: Python
class Solution:
    def splitListToParts(self, root: ListNode, k: int) -> List[ListNode]:
        ans = [None for i in range(k)]
        ans[0] = root
        # 初始化指针数组，按顺序指向前k个结点
        for i in range(1, k):
            if ans[i - 1]:
                ans[i] = ans[i - 1].next
        # 移动指针，数组下标为 i 的指针每次前进 i + 1
        while ans[k - 1]:
            for i in range(k-1):
                ans[k - 1] = ans[k - 1].next
                if not ans[k - 1]:
                    break
                for j in range(i, k - 1):
                    ans[j] = ans[j].next
            if ans[k - 1]:
                ans[k - 1] = ans[k - 1].next
        # 此时链表已经由 k - 1 个指针划分为 k 段，数组中的指针均指向各段最后一个结点
        # 将链表分割成 k 段，并将数组指针设为各段的头结点, 即上一段最后一个结点的next指针指向的结点
        for i in range(k - 1, 0, -1):
            if ans[i - 1]:
                ans[i] = ans[i - 1].next
                ans[i - 1].next = None
        # 第一段的头结点为 root
        ans[0] = root
        return ans

复杂度

  • 时间复杂度：\(O(n * k)\), n 为链表长度，平均每个指针前进了 \(\frac{1}{2}n\) 的距离，总共 K 个指针
  • 空间复杂度：\(O(k)\), 仅答案数组的空间，不计算答案的空间则为 \(O(1)\)
--- ♥ end ♥ ---

欢迎关注我呀~