小鲸鱼的梦境
0%

『LeetCode』198 打家劫舍

发表于 更新于 分类于 Valine：
本文字数： 5.7k 阅读时长 ≈ 5 分钟

题目

198. 打家劫舍

难度: 中等

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

\(\quad\)

示例 1：

输入： [1,2,3,1]
输出： 4
解释： 偷窃 1 号房屋 (金额 = 1) ，然后偷窃 3 号房屋 (金额 = 3)。
\(\qquad\) 偷窃到的最高金额 = 1 + 3 = 4 。

示例 2：

输入： [2,7,9,3,1]
输出： 12
解释： 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9)，接着偷窃 5 号房屋 (金额 = 1)。
\(\qquad\) 偷窃到的最高金额 = 2 + 9 + 1 = 12 。

提示：

  • 1 <= nums.length <= 100
  • 0 <= nums[i] <= 400

解析

深度优先搜索

对于这道题最简单的想法就是，遍历所有可能的情况，找出可能的最大值。

具体来说就是，对第一个房屋，考虑偷和不偷两种情况，对于第二个房屋，考虑偷和不偷两种情况，但如果第一个房屋偷过了，那么第二个房屋的选择只能是不偷，所以此时有三种情况（偷房屋1不偷房屋2，不偷房屋1不偷房屋2，不偷房屋1不偷房屋2），以此类推，到最后一间房屋我们就能穷举所有的可能。

对于四间房屋的所有可能性如下图：

dfs

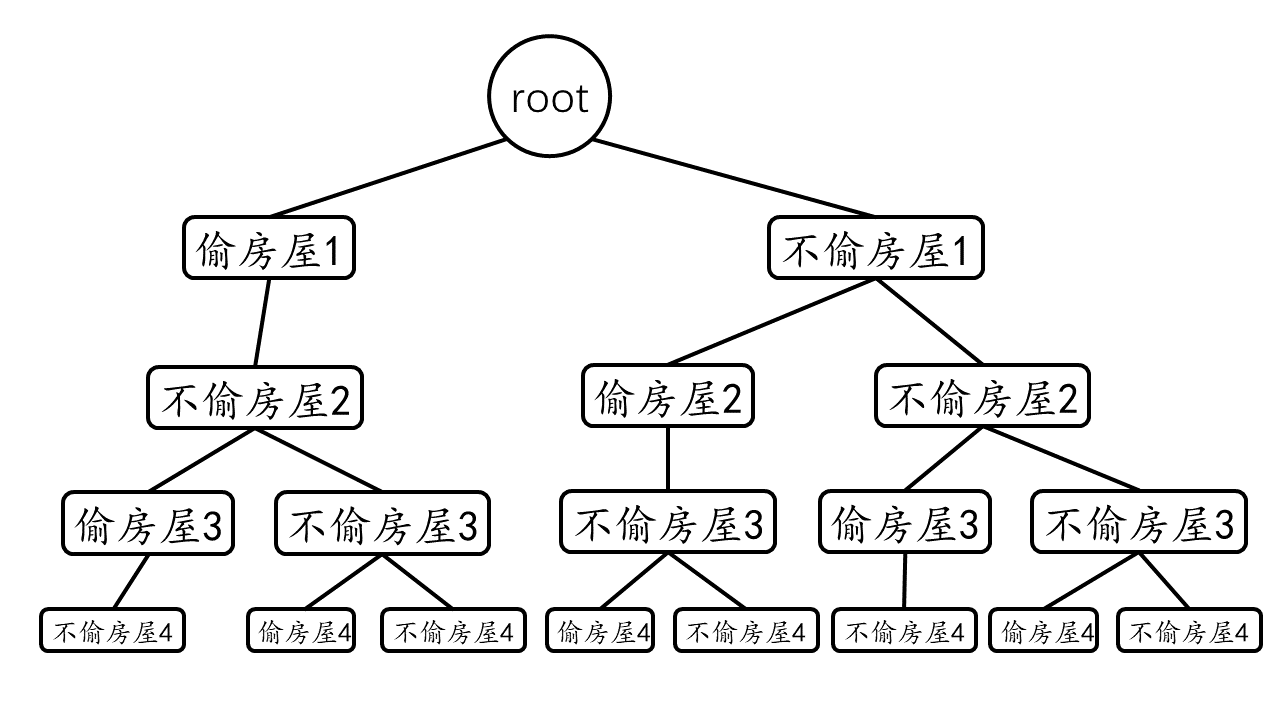
由此我们很容易就能得到递归的遍历方式

  1. 递归函数返回值为从第i个房屋开始包括第i个房屋在内的房屋所能偷窃的最大值
  2. 递归函数需要传入的参数为房屋位置i以及标记issteal标记第i-1个房屋是否被偷过
  3. 递归函数需要做的仅仅是根据i-1个房屋是否偷过决定能否偷第i个房屋，而第i+1及之后的房屋可以通过递归计算得到

这种dfs穷举法的时间复杂度是指数级的，对于长度范围为100的测试用例是肯定会超TLE的。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
/* Code language: C++ */
class Solution {
public:
    /* dfs */
    int rob(vector<int>& nums) {
        return dfs(nums, 0, false);
    }

    /* 返回第i个房屋及之后能偷窃到的最大值，issteal标志第i - 1个房屋是否偷窃 */
    int dfs(vector<int>& nums, int i, bool issteal) {
        /* i越界，没房屋可供偷窃，只能空手而归了>_< */
        if (i >= nums.size()) return 0;
        /* 前一个偷过了，那这个就不能偷了！去下一家看看~ */
        else if (issteal)
            return dfs(nums, i + 1, false);
        /* 前一个没偷过，那么这个可偷可不偷，两者取大的那个 */
        else
            return max(dfs(nums, i + 1, true) + nums[i], dfs(nums, i + 1, false));
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# Code language: Python
class Solution:
    # 朴素dfs
    def rob(self, nums: List[int]) -> int:
        n = len(nums)

        # 返回第i个房屋及之后能偷窃到的最大值，issteal标志第i - 1个房屋是否偷窃
        def dfs(i, issteal):
            # i越界，没房屋可供偷窃，只能空手而归了>_<
            if i >= n:
                return 0
            # 前一个偷过了，那这个就不能偷了！去下一家看看~
            elif issteal:
                return dfs(i + 1, False)
            # 前一个没偷过，那么这个可偷可不偷，两者取大的那个
            else:
                return max(dfs(i + 1, True) + nums[i], dfs(i + 1, False))

        return dfs(0, False)
  • 时间复杂度：\(O(f(n))\), 其中 \(f(n)\) 是指Fibonacci数列第n项，这是指数级别的复杂度
  • 空间复杂度：\(O(n)\), 递归的最大深度为 n

时间复杂度计算如下, 其中 \(T(i-0)\) 表示偷第i个房屋, \(T(i-1)\)表示不偷第i个房屋, \(f_n\) 表示第n个Fibonacci数

\[ \begin{split} T(0){} & = T(1-0) + T(1-1)\\\\ & = T(2-1) + (T(2-0) + T(2-1))\\\\ & = T(2-0) + 2T(2-1)\\\\ & = T(3-1) + 2(T(3-0) + T(3-1))\\\\ & = 2T(3-0) + 3T(3-1)\\\\ & = 3T(4-0) + 5T(4-1)\\\\ & \dots\dots\\\\ & = f_nT(n-0) + f_{n - 1}T(n-1) \end{split} \]

记忆化dfs

从dfs的示意图和时间复杂度的计算中都可以看出，在dfs的执行过程中是有大量的重复计算的，这里和用递归的方式计算Fibonacci数是类似的，例如偷房屋4计算了3次、不偷房屋4计算了5次，这些重复计算在数据增多的时候会呈指数级的增长。针对这个问题，有一种通用的解决方法：申请一块空间专门用于缓存，将计算结果保存到缓存中，下次调用递归前先检查缓存中是否存在计算过的值，如果存在那么就无需再次计算可以直接从缓存中获取结果从而避免了重复计算。如下图所示：

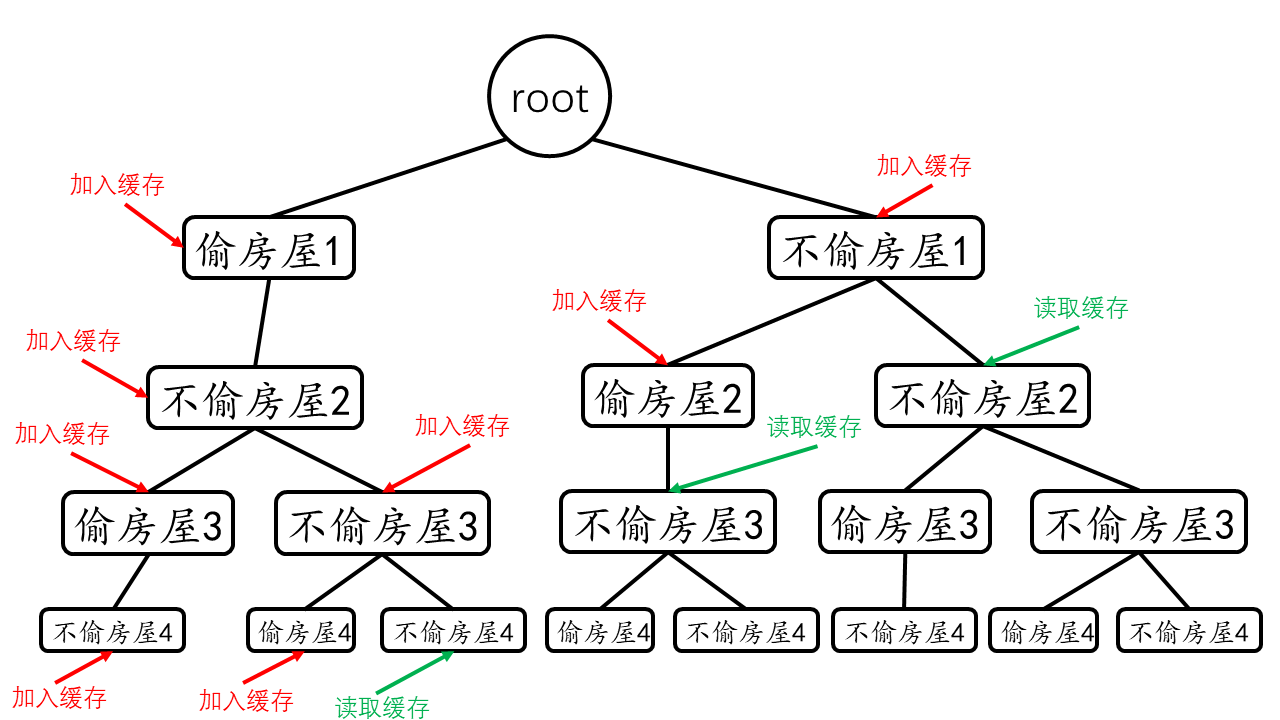
记忆化dfs

通过记忆化的方法，我们在递归计算时缓存计算的值，而在调用递归函数前先检测缓存中是否存在，不存在才进行计算(python 可以使用装饰器lru_cache完成记忆化的功能)

其中，两个缓存数组分别记录偷与不偷第i个房屋的情况下第i个房屋及之后能偷窃到的最大值，数组长度设为109是因为nums的长度最大为100，所以设置缓存数组长度要比nums长度稍微大一些，如果nums长度不确定，也可以使用vector<int>代替

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
/* Code language: C++ */
class Solution {
public:
    /* 记忆化dfs */
    /* 两个数组分别记录偷与不偷第i个房屋的情况下第i个房屋及之后能偷窃到的最大值 */
    /* 初始值设置为-1，表示不偷 */
    int st[107], nst[107];
    int rob(vector<int>& nums) {
        /* 初始化缓存数组 */
        for (int i = 0; i < nums.size(); ++i) {
            st[i]  = -1;
            nst[i] = -1;
        }
        return dfs(nums, 0, false);
    }

    /* 返回第i个房屋及之后能偷窃到的最大值，issteal标志第i - 1个房屋是否偷窃 */
    int dfs(vector<int>& nums, int i, bool issteal) {
        /* i越界，没房屋可供偷窃，只能空手而归了>_< */
        if (i >= nums.size()) return 0;
        /* 前一个偷过了，那这个就不能偷了！去下一家看看~ */
        else if (issteal) {
            if (nst[i + 1] == -1) nst[i + 1] = dfs(nums, i + 1, false);
            return nst[i + 1];
        }
        /* 前一个没偷过，那么这个可偷可不偷，两者取大的那个 */
        else {
            if (st[i + 1] == -1) st[i + 1] = dfs(nums, i + 1, true);
            if (nst[i + 1] == -1) nst[i + 1] = dfs(nums, i + 1, false);
            return max(st[i + 1] + nums[i], nst[i + 1]);
        }
    }
};
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
# Code language: Python
from functools import lru_cache
class Solution:
    # 记忆化dfs
    def rob(self, nums: List[int]) -> int:
        n = len(nums)

        # 返回第i个房屋及之后能偷窃到的最大值，issteal标志第i - 1个房屋是否偷窃
        @lru_cache(None) # 装饰器，用于缓存，None表示不限制缓存大小
        def dfs(i, issteal):
            # i越界，没房屋可供偷窃，只能空手而归了>_<
            if i >= n:
                return 0
            # 前一个偷过了，那这个就不能偷了！去下一家看看~
            elif issteal:
                return dfs(i + 1, False)
            # 前一个没偷过，那么这个可偷可不偷，两者取大的那个
            else:
                return max(dfs(i + 1, True) + nums[i], dfs(i + 1, False))

        return dfs(0, False)
  • 时间复杂度: \(O(n)\) 最多只需将两个缓存数组填满就能得到结果
  • 空间复杂度: \(O(n)\) 缓存数组长度

动态规划

考察记忆化dfs的计算过程，

  • 若i - 1间房屋偷窃过了，那么第i间房屋就不能偷窃了，而从第i+1间房屋开始考察，则又回到了问题的起点：从第i+1间房屋开始的街道最多能偷窃到的金额，和最初的原问题相比仅仅是规模缩小了
  • 同理，若i-1间房屋没有偷窃过，那么同样是回到了问题的起点，和上一个的区别仅仅是起点是从i间房屋开始的街道最多能偷窃到的金额

由此我们可以得到一个将大规模的问题转换到规模更小的同样的问题的递推公式

\[ \begin{split} &(1) \quad nst[i] = st[i + 1] \\\\ &(2) \quad st[i] = max(nst[i + 1] + nums[i], st[i + 1]) \end{split} \]

注意在(1)式中 \(nst\) 可以由 \(st\) 通过下标偏移得到，所以就可以消去 \(nst\) 数组，递推公式如下：

\[ st[i] = max(st[i + 2] + nums[i], st[i + 1]) \]

由此递推公式很容易就能在 \(O(n)\) 的时间复杂度内由后往前的计算出 \(st[0]\) 的值，\(st[0]\) 表示的是从第0间房屋开始能偷窃到的最大值，即原问题本身，也是我们要求解的。

但是由后向前偷不符合小偷的习惯，我们换一种更容易理解的方法来重复一遍解答过程：

  • dp[i] 表示前i间房屋能偷取到的最大值
  • dp[i] = max(dp[i - 1], dp[i - 2] + nums[i])
  • 递推公式的含义是：前i间房屋能偷取到的最大值考虑两种情况，取大的那个
    1. 不偷第i间房屋，那么前i间房屋能偷取的金额等于dp[i - 1] (即前i - 1间房屋能偷取到的最大值)
    2. 偷取第i间房屋，那么第i - 1间房屋就无法偷取了，所以前i间房屋能偷取的金额等于dp[i - 2] (即前i - 2间房屋能偷取到的最大值) 与 第i间房屋能偷取的金额之和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
/* Code language: C++ */
class Solution {
public:
    /* 动态规划 */
    /* dp[i] 表示前i个房屋所能偷到的最大值 */
    int dp[109];
    int rob(vector<int>& nums) {
        int n = nums.size();
        dp[0] = nums[0];
        dp[1] = max(nums[0], n > 1 ? nums[1] : 0);
        for (int i = 2; i < n; ++i)
            dp[i] = max(dp[i - 1], dp[i - 2] + nums[i]);
        return dp[n - 1];
    }
};
1
2
3
4
5
6
7
8
# Code language: Python
class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        dp = [nums[0], max(nums[0], nums[1] if n > 1 else 0)]
        for i in range(2, n):
            dp.append(max(dp[i - 1], dp[i - 2] + nums[i]))
        return dp[-1]
  • 时间复杂度: \(O(n)\), 遍历一次nums数组即可
  • 空间复杂度: \(O(n)\), dp数组的长度为n

滚动数组优化

注意到 dp[i] 仅仅与 dp[i - 1] 和 dp[i - 2] 的值有关，所以可以无需保存 dp[i - 2] 之前的值，即使用三个变量分别保存 dp[i - 2], dp[i - 1], dp[i] 再不断迭代更新即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
/* Code language: C++ */
class Solution {
public:
    /* 动态规划 + 滚动数组 */
    /* x, y, z 分别表示前i - 2， i - 1, i个房屋所能偷到的最大值 */
    int rob(vector<int>& nums) {
        int n = nums.size();
        int x = nums[0], y = max(nums[0], n > 1 ? nums[1] : 0), z;
        for (int i = 2; i < n; ++i) {
            z = max(x + nums[i], y);
            x = y;
            y = z;
        }
        return y;
    }
};
1
2
3
4
5
6
7
8
9
# Code language: Python
class Solution:
    def rob(self, nums: List[int]) -> int:
        n = len(nums)
        # x, y 分别表示前i - 1， i个房屋所能偷到的最大值
        x, y = nums[0], max(nums[0], nums[1] if n > 1 else 0)
        for i in range(2, n):
            x, y = y, max(x + nums[i], y)
        return y
  • 时间复杂度: \(O(n)\), 遍历一次nums数组即可
  • 空间复杂度: \(O(1)\), 只使用了常数个变量
--- ♥ end ♥ ---

欢迎关注我呀~